Question Number 29778 by puneet1789 last updated on 12/Feb/18
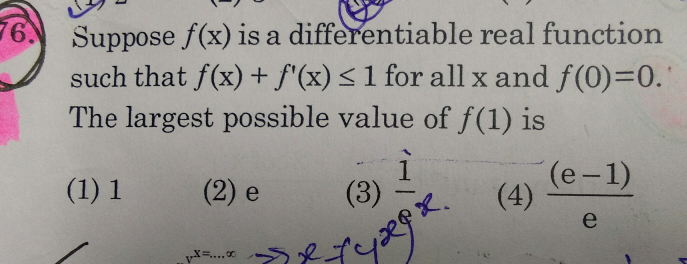
Answered by Giannibo last updated on 12/Feb/18
![f(x)+f′(x)≤1 e^x f(x)+e^x f′(x)≤e^x ∫_0 ^1 (e^x f(x))′dx≤∫_0 ^1 e^x dx [e^x f(x)]_0 ^1 ≤[e^x ]_0 ^1 ef(1)−f(0)≤e−1 f(1)≤((e−1)/e)](https://www.tinkutara.com/question/Q29788.png)
$$ \\ $$$$ \\ $$$$\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}'\left(\mathrm{x}\right)\leqslant\mathrm{1} \\ $$$$\mathrm{e}^{\mathrm{x}} \mathrm{f}\left(\mathrm{x}\right)+\mathrm{e}^{\mathrm{x}} \mathrm{f}'\left(\mathrm{x}\right)\leqslant\mathrm{e}^{\mathrm{x}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{e}^{\mathrm{x}} \mathrm{f}\left(\mathrm{x}\right)\right)'\mathrm{dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{e}^{\mathrm{x}} \mathrm{dx} \\ $$$$\left[\mathrm{e}^{\mathrm{x}} \mathrm{f}\left(\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \leqslant\left[\mathrm{e}^{\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{ef}\left(\mathrm{1}\right)−\mathrm{f}\left(\mathrm{0}\right)\leqslant\mathrm{e}−\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)\leqslant\frac{\mathrm{e}−\mathrm{1}}{\mathrm{e}} \\ $$
