Question Number 29803 by ajfour last updated on 12/Feb/18

Commented by ajfour last updated on 12/Feb/18
Commented by ajfour last updated on 12/Feb/18
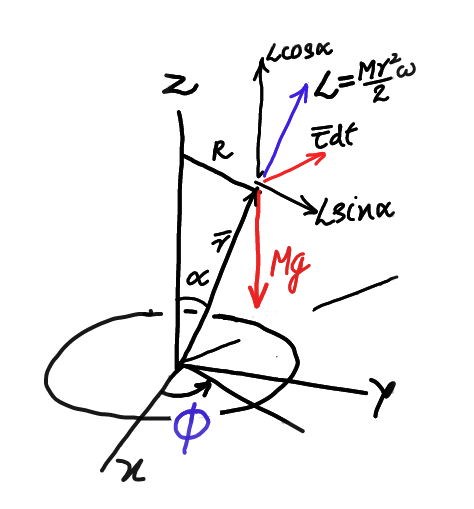
![𝛕^� =r^� ×M g^� =[R(cos 𝛗i^� +sin 𝛗j^� )+(Rcot α)k^� ]×(−Mg k^� ) L^� = Iωsin α(cos 𝛗i^� +sin 𝛗j^� ) +(Iωcos α) k^� from 𝛕^� = (dL^� /dt) , we get MgR(−sin 𝛗i^� +cos 𝛗j^� ) = Iωsin α(−sin 𝛗i^� +cos 𝛗j^� )(d𝛗/dt) ⇒ (d𝛗/dt) = Ω = ((MgR)/(Iωsin α)) or 𝛀^� =((MgR)/((((Mr^2 ωsin α)/2))))k^� 𝛀^� = ((2gR)/(ωr^2 sin α)) k^� ⇒ 𝛕^� = 𝛀^� ×I𝛚^� MgR = (((2gR)/(ωr^2 sin α)))(((Mr^2 )/2))ωsin α The direction even is consistent.](https://www.tinkutara.com/question/Q29817.png)
$$\:\:\bar {\boldsymbol{\tau}}\:=\bar {\boldsymbol{{r}}}×{M}\:\bar {\boldsymbol{{g}}} \\ $$$$\:\:\:\:\:\:=\left[{R}\left(\mathrm{cos}\:\boldsymbol{\phi}\hat {{i}}+\mathrm{sin}\:\boldsymbol{\phi}\hat {{j}}\right)+\left({R}\mathrm{cot}\:\alpha\right)\hat {{k}}\right]×\left(−{Mg}\:\hat {{k}}\right) \\ $$$$\:\:\bar {\boldsymbol{{L}}}\:=\:{I}\omega\mathrm{sin}\:\alpha\left(\mathrm{cos}\:\boldsymbol{\phi}\hat {{i}}+\mathrm{sin}\:\boldsymbol{\phi}\hat {{j}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({I}\omega\mathrm{cos}\:\alpha\right)\:\hat {{k}} \\ $$$${from}\:\:\:\:\bar {\boldsymbol{\tau}}\:\:=\:\frac{{d}\bar {{L}}}{{dt}}\:\:,\:{we}\:{get} \\ $$$$\:\:{MgR}\left(−\mathrm{sin}\:\boldsymbol{\phi}\hat {{i}}+\mathrm{cos}\:\boldsymbol{\phi}\hat {{j}}\right)\:= \\ $$$$\:\:\:{I}\omega\mathrm{sin}\:\alpha\left(−\mathrm{sin}\:\boldsymbol{\phi}\hat {{i}}+\mathrm{cos}\:\boldsymbol{\phi}\hat {{j}}\right)\frac{{d}\boldsymbol{\phi}}{{dt}} \\ $$$$\Rightarrow\:\:\:\:\frac{{d}\boldsymbol{\phi}}{{dt}}\:=\:\Omega\:=\:\frac{{MgR}}{{I}\omega\mathrm{sin}\:\alpha} \\ $$$${or}\:\:\:\:\:\:\:\bar {\boldsymbol{\Omega}}\:=\frac{{MgR}}{\left(\frac{{Mr}^{\mathrm{2}} \omega\mathrm{sin}\:\alpha}{\mathrm{2}}\right)}\hat {{k}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\bar {\boldsymbol{\Omega}}\:=\:\frac{\mathrm{2}{gR}}{\omega{r}^{\mathrm{2}} \mathrm{sin}\:\alpha}\:\hat {{k}} \\ $$$$\:\:\:\Rightarrow\:\:\:\:\bar {\boldsymbol{\tau}}\:\:=\:\bar {\boldsymbol{\Omega}}×\boldsymbol{{I}}\bar {\boldsymbol{\omega}}\:\:\: \\ $$$$\:{MgR}\:=\:\left(\frac{\mathrm{2}{gR}}{\omega{r}^{\mathrm{2}} \mathrm{sin}\:\alpha}\right)\left(\frac{{Mr}^{\mathrm{2}} }{\mathrm{2}}\right)\omega\mathrm{sin}\:\alpha \\ $$$${The}\:{direction}\:{even}\:{is}\:{consistent}.\: \\ $$
Commented by ajfour last updated on 13/Feb/18

$${Find}\:\Omega\:{in}\:{terms}\:{of}\:{M},{r},{R},\omega,\:\alpha \\ $$$${given}\:\alpha\:{stays}\:{constant}. \\ $$$${What}\:{is}\:\theta=\alpha\left({t}\right),\:\Omega\left({t}\right)\:{in}\:{terms}\:{of} \\ $$$$\frac{{d}\omega}{{dt}}\:? \\ $$
