Question Number 29887 by naka3546 last updated on 13/Feb/18
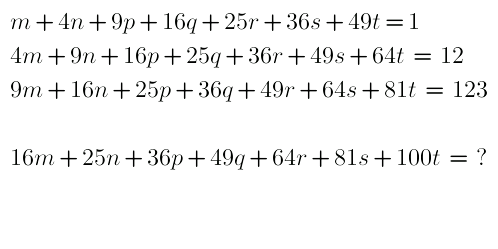
Commented by 803jaideep@gmail.com last updated on 13/Feb/18

$$\mathrm{1234}? \\ $$
Commented by naka3546 last updated on 13/Feb/18

$${are}\:{you}\:{sure}\:\:? \\ $$
Commented by 803jaideep@gmail.com last updated on 13/Feb/18

$$\mathrm{no}…\mathrm{i}\:\mathrm{just}\:\mathrm{guessed}\:\mathrm{from}\:\mathrm{the}\:\mathrm{series}\: \\ $$$$\mathrm{answers}…\:\mathrm{i}\:\mathrm{dnt}\:\mathrm{knw}\:\mathrm{abt}\:\mathrm{it} \\ $$
Answered by ajfour last updated on 13/Feb/18

$${a}+\mathrm{4}{b}+\mathrm{9}{c}=\mathrm{16}\:\:\:\:\:\:\:…\left({i}\right) \\ $$$$\mathrm{4}{a}+\mathrm{9}{b}+\mathrm{16}{c}=\mathrm{25}\:\:\:\:\:\:\:…..\left({ii}\right) \\ $$$$\mathrm{9}{a}+\mathrm{16}{b}+\mathrm{25}{c}=\mathrm{36}\:\:\:\:\:\:\:……\left({iii}\right) \\ $$$${and}\:{even}\:\:\mathrm{16}{a}+\mathrm{25}{b}+\mathrm{36}{c}=\mathrm{49} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{25}{a}+\mathrm{36}{b}+\mathrm{49}{c}=\mathrm{64} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{36}{a}+\mathrm{49}{b}+\mathrm{64}{c}=\mathrm{81} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{49}{a}+\mathrm{64}{b}+\mathrm{81}{c}=\mathrm{100} \\ $$$$\left({iii}\right)−\left({i}\right)−\left({ii}\right)\:{gives} \\ $$$$\:\:\:\mathrm{4}{a}+\mathrm{3}{b}\:=−\mathrm{5}\:\:\:\:\:\:\:…..\left({I}\right) \\ $$$$\mathrm{9}×\left({ii}\right)−\mathrm{16}×\left({i}\right)\:{gives} \\ $$$$\:\:\:\mathrm{20}{a}+\mathrm{17}{b}=\:−\mathrm{31}\:\:\:\:\:\:…..\left({II}\right) \\ $$$$\left({II}\right)−\mathrm{5}×\left({I}\right)\:{gives} \\ $$$$\:\:\:\:\:\mathrm{2}{b}\:=\:−\mathrm{6}\:\:\:\Rightarrow\:\:\:{b}=−\mathrm{3} \\ $$$$\:\:\:{then}\:\:{from}\:\left({I}\right), \\ $$$$\:\:\:\:\:\:\mathrm{4}{a}−\mathrm{9}\:=\:−\mathrm{5}\:\:\:\Rightarrow\:\:\:{a}=\mathrm{1} \\ $$$${And}\:\:{from}\:\left({i}\right), \\ $$$$\:\:\:\mathrm{1}−\mathrm{12}+\mathrm{9}{c}\:=\:\mathrm{16}\:\:\:\Rightarrow\:\:{c}\:=\:\mathrm{3} \\ $$$$\Rightarrow\:\:{l}.{h}.{s}.\:{of}\:{eq}.\:{in}\:{question} \\ $$$$\:\:\:\:\:\:=\:\mathrm{1}−\mathrm{3}\left(\mathrm{12}\right)+\mathrm{3}\left(\mathrm{123}\right)\: \\ $$$$\:\:\:\:\:=\:\mathrm{334}\:. \\ $$
Commented by MJS last updated on 14/Feb/18
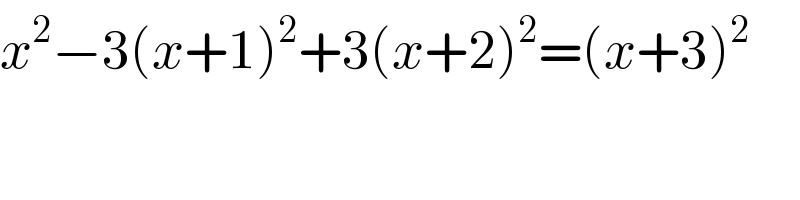
$${x}^{\mathrm{2}} −\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\left({x}+\mathrm{2}\right)^{\mathrm{2}} =\left({x}+\mathrm{3}\right)^{\mathrm{2}} \\ $$
