Question Number 29924 by ajfour last updated on 13/Feb/18
Commented by ajfour last updated on 13/Feb/18

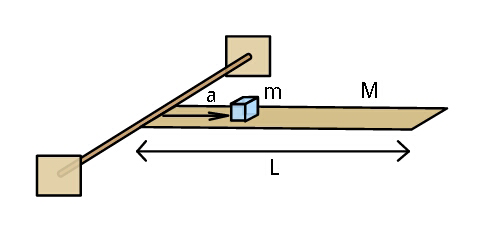
$${On}\:{a}\:{plank}\:{a}\:{small}\:{block}\:{m}\:{is} \\ $$$${kept}.\:{The}\:{plank}\:{is}\:{free}\:{to}\:{rotate} \\ $$$${about}\:{a}\:{horizontal}\:{axis}\:{at}\:{its}\:{end}. \\ $$$${If}\:{released}\:{as}\:{shown},\:{find} \\ $$$${angle},\:{angular}\:{velocity}\:{of}\:{plank} \\ $$$${when}\:{normal}\:{reaction}\:{between} \\ $$$${plank}\:{and}\:{block}\:{becomes}\:{zero}. \\ $$$$\left({Assume}\:{friction}\:{coefficient}\:\boldsymbol{\mu}\right). \\ $$
Commented by 33 last updated on 13/Feb/18

$${nice}\:{question}\:{sir} \\ $$
Commented by ajfour last updated on 13/Feb/18
Commented by mrW2 last updated on 15/Feb/18

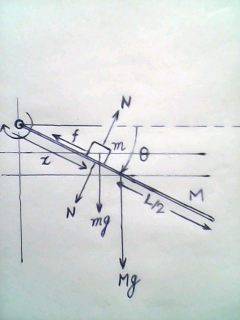
$${the}\:{normal}\:{force}\:{gets}\:{to}\:{zero},\:{when} \\ $$$${the}\:{block}\:{reaches}\:{the}\:{position}\:{x}=\frac{\mathrm{2}{L}}{\mathrm{3}}. \\ $$$${But}\:{the}\:{coresponding}\:{angle}\:{positio}\:\theta \\ $$$${seems}\:{not}\:{to}\:{be}\:{in}\:{relation}\:{with}\:{x}, \\ $$$${therefore}\:{I}\:{have}\:{no}\:{solution}. \\ $$
Commented by ajfour last updated on 15/Feb/18
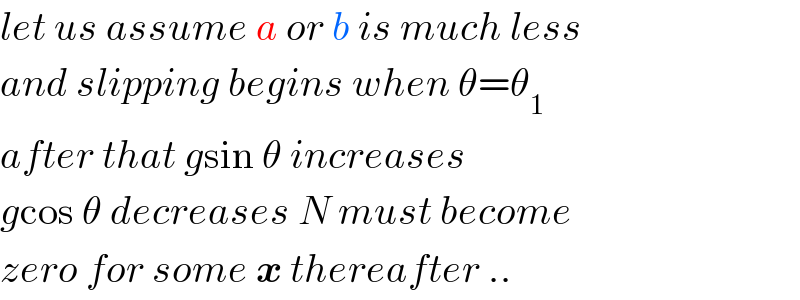
$${let}\:{us}\:{assume}\:{a}\:{or}\:{b}\:{is}\:{much}\:{less} \\ $$$${and}\:{slipping}\:{begins}\:{when}\:\theta=\theta_{\mathrm{1}} \\ $$$${after}\:{that}\:{g}\mathrm{sin}\:\theta\:{increases} \\ $$$${g}\mathrm{cos}\:\theta\:{decreases}\:{N}\:{must}\:{become} \\ $$$${zero}\:{for}\:{some}\:\boldsymbol{{x}}\:{thereafter}\:.. \\ $$
Answered by mrW2 last updated on 13/Feb/18

Commented by mrW2 last updated on 14/Feb/18
![phase 1: no slip between block and plank x=b=constant (b replaces a in question) ω=(dθ/dt) α=(dω/dt) v_θ =xω=bω v_r =(dx/dt)=0 mg cos θ−N=mbα ⇒N=m(g cos θ−bα) f−mg sin θ=mbω^2 ⇒f=m(g sin θ+bω^2 ) ((ML^2 )/3)α=Nb+Mg((Lcos θ)/2) ((ML^2 )/3)α=mb(g cos θ−bα)+Mg((Lcos θ)/2) (((ML^2 +3mb^2 )/3))α=(((2mb+ML)gcos θ)/2) ⇒α=((3(2mb+ML)g)/(2(ML^2 +3mb^2 )))cos θ ⇒ω(dω/dθ)=((3(2mb+ML)g)/(2(ML^2 +3mb^2 )))cos θ ⇒∫_0 ^ω ωdω=((3(2mb+ML)g)/(2(ML^2 +3mb^2 )))∫_0 ^θ cos θ dθ ⇒(ω^2 /2)=((3(2mb+ML)g)/(2(ML^2 +3mb^2 ))) sin θ ⇒ω^2 =((3(2mb+ML)g)/((ML^2 +3mb^2 ))) sin θ ⇒f=mg[1+((3b(2mb+ML))/((ML^2 +3mb^2 )))]sin θ ⇒f=[((ML^2 +9mb^2 +3MLb)/(ML^2 +3mb^2 ))]mg sin θ ⇒N=mg[1−((3b(2mb+ML))/(2(ML^2 +3mb^2 )))]cos θ ⇒N=[((ML(2L−3b))/(2(ML^2 +3mb^2 )))]mg cos θ (f/N)=((ML^2 +9mb^2 +3MLb)/(ML^2 +3mb^2 ))×((2(ML^2 +3mb^2 ))/(ML(2L−3b)))×tan θ ⇒(f/N)=((2(ML^2 +9mb^2 +3MLb))/(ML(2L−3b)))×tan θ=μ tan θ_1 =((μML(2L−3b))/(2(ML^2 +9mb^2 +3MLb))) θ_1 =tan^(−1) {((μML(2L−3b))/(2(ML^2 +9mb^2 +3MLb)))} with η=(m/M) and λ=(b/L) ⇒θ_1 =tan^(−1) {((μ(2−3λ))/(2(1+3λ+9ηλ^2 )))} i.e. at θ=θ_1 block m begins to slip. E.g. η=(m/M)=0.5, λ=(b/L)=0.25, μ=1 ⇒θ_1 =tan^(−1) {((1×(2−3×0.25))/(2(1+3×0.25+9×0.5×0.25^2 )))}=17.1° at θ=θ_1 : N_1 =[((2−3λ)/(2(1+3ηλ^2 )))]mg cos θ_1 ω_1 =(√(((3(1+2ηλ)g)/(L(1+3ηλ^2 ))) sin θ_1 )) in phase 1 the reaction force N is always more than zero if λ<(2/3), i.e. if b<(2/3)L.](https://www.tinkutara.com/question/Q29939.png)
$${phase}\:\mathrm{1}:\:{no}\:{slip}\:{between}\:{block}\:{and}\:{plank} \\ $$$${x}={b}={constant}\:\left({b}\:{replaces}\:{a}\:{in}\:{question}\right) \\ $$$$\omega=\frac{{d}\theta}{{dt}} \\ $$$$\alpha=\frac{{d}\omega}{{dt}} \\ $$$${v}_{\theta} ={x}\omega={b}\omega \\ $$$${v}_{{r}} =\frac{{dx}}{{dt}}=\mathrm{0} \\ $$$${mg}\:\mathrm{cos}\:\theta−{N}={mb}\alpha \\ $$$$\Rightarrow{N}={m}\left({g}\:\mathrm{cos}\:\theta−{b}\alpha\right) \\ $$$${f}−{mg}\:\mathrm{sin}\:\theta={mb}\omega^{\mathrm{2}} \\ $$$$\Rightarrow{f}={m}\left({g}\:\mathrm{sin}\:\theta+{b}\omega^{\mathrm{2}} \right) \\ $$$$\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}\alpha={Nb}+{Mg}\frac{{L}\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$$\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}\alpha={mb}\left({g}\:\mathrm{cos}\:\theta−{b}\alpha\right)+{Mg}\frac{{L}\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$$\left(\frac{{ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} }{\mathrm{3}}\right)\alpha=\frac{\left(\mathrm{2}{mb}+{ML}\right){g}\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow\alpha=\frac{\mathrm{3}\left(\mathrm{2}{mb}+{ML}\right){g}}{\mathrm{2}\left({ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} \right)}\mathrm{cos}\:\theta \\ $$$$\Rightarrow\omega\frac{{d}\omega}{{d}\theta}=\frac{\mathrm{3}\left(\mathrm{2}{mb}+{ML}\right){g}}{\mathrm{2}\left({ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} \right)}\mathrm{cos}\:\theta \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\omega} \omega{d}\omega=\frac{\mathrm{3}\left(\mathrm{2}{mb}+{ML}\right){g}}{\mathrm{2}\left({ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} \right)}\int_{\mathrm{0}} ^{\theta} \mathrm{cos}\:\theta\:{d}\theta \\ $$$$\Rightarrow\frac{\omega^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{3}\left(\mathrm{2}{mb}+{ML}\right){g}}{\mathrm{2}\left({ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} \right)}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\omega^{\mathrm{2}} =\frac{\mathrm{3}\left(\mathrm{2}{mb}+{ML}\right){g}}{\left({ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} \right)}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{f}={mg}\left[\mathrm{1}+\frac{\mathrm{3}{b}\left(\mathrm{2}{mb}+{ML}\right)}{\left({ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} \right)}\right]\mathrm{sin}\:\theta \\ $$$$\Rightarrow{f}=\left[\frac{{ML}^{\mathrm{2}} +\mathrm{9}{mb}^{\mathrm{2}} +\mathrm{3}{MLb}}{{ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} }\right]{mg}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{N}={mg}\left[\mathrm{1}−\frac{\mathrm{3}{b}\left(\mathrm{2}{mb}+{ML}\right)}{\mathrm{2}\left({ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} \right)}\right]\mathrm{cos}\:\theta \\ $$$$\Rightarrow{N}=\left[\frac{{ML}\left(\mathrm{2}{L}−\mathrm{3}{b}\right)}{\mathrm{2}\left({ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} \right)}\right]{mg}\:\mathrm{cos}\:\theta \\ $$$$\frac{{f}}{{N}}=\frac{{ML}^{\mathrm{2}} +\mathrm{9}{mb}^{\mathrm{2}} +\mathrm{3}{MLb}}{{ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} }×\frac{\mathrm{2}\left({ML}^{\mathrm{2}} +\mathrm{3}{mb}^{\mathrm{2}} \right)}{{ML}\left(\mathrm{2}{L}−\mathrm{3}{b}\right)}×\mathrm{tan}\:\theta \\ $$$$\Rightarrow\frac{{f}}{{N}}=\frac{\mathrm{2}\left({ML}^{\mathrm{2}} +\mathrm{9}{mb}^{\mathrm{2}} +\mathrm{3}{MLb}\right)}{{ML}\left(\mathrm{2}{L}−\mathrm{3}{b}\right)}×\mathrm{tan}\:\theta=\mu \\ $$$$\mathrm{tan}\:\theta_{\mathrm{1}} =\frac{\mu{ML}\left(\mathrm{2}{L}−\mathrm{3}{b}\right)}{\mathrm{2}\left({ML}^{\mathrm{2}} +\mathrm{9}{mb}^{\mathrm{2}} +\mathrm{3}{MLb}\right)} \\ $$$$\theta_{\mathrm{1}} =\mathrm{tan}^{−\mathrm{1}} \left\{\frac{\mu{ML}\left(\mathrm{2}{L}−\mathrm{3}{b}\right)}{\mathrm{2}\left({ML}^{\mathrm{2}} +\mathrm{9}{mb}^{\mathrm{2}} +\mathrm{3}{MLb}\right)}\right\} \\ $$$${with}\:\eta=\frac{{m}}{{M}}\:{and}\:\lambda=\frac{{b}}{{L}} \\ $$$$\Rightarrow\theta_{\mathrm{1}} =\mathrm{tan}^{−\mathrm{1}} \left\{\frac{\mu\left(\mathrm{2}−\mathrm{3}\lambda\right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{3}\lambda+\mathrm{9}\eta\lambda^{\mathrm{2}} \right)}\right\} \\ $$$${i}.{e}.\:{at}\:\theta=\theta_{\mathrm{1}} \:{block}\:{m}\:{begins}\:{to}\:{slip}. \\ $$$${E}.{g}.\:\eta=\frac{{m}}{{M}}=\mathrm{0}.\mathrm{5},\:\lambda=\frac{{b}}{{L}}=\mathrm{0}.\mathrm{25},\:\mu=\mathrm{1} \\ $$$$\Rightarrow\theta_{\mathrm{1}} =\mathrm{tan}^{−\mathrm{1}} \left\{\frac{\mathrm{1}×\left(\mathrm{2}−\mathrm{3}×\mathrm{0}.\mathrm{25}\right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{3}×\mathrm{0}.\mathrm{25}+\mathrm{9}×\mathrm{0}.\mathrm{5}×\mathrm{0}.\mathrm{25}^{\mathrm{2}} \right)}\right\}=\mathrm{17}.\mathrm{1}° \\ $$$$ \\ $$$${at}\:\theta=\theta_{\mathrm{1}} : \\ $$$${N}_{\mathrm{1}} =\left[\frac{\mathrm{2}−\mathrm{3}\lambda}{\mathrm{2}\left(\mathrm{1}+\mathrm{3}\eta\lambda^{\mathrm{2}} \right)}\right]{mg}\:\mathrm{cos}\:\theta_{\mathrm{1}} \\ $$$$\omega_{\mathrm{1}} =\sqrt{\frac{\mathrm{3}\left(\mathrm{1}+\mathrm{2}\eta\lambda\right){g}}{{L}\left(\mathrm{1}+\mathrm{3}\eta\lambda^{\mathrm{2}} \right)}\:\mathrm{sin}\:\theta_{\mathrm{1}} } \\ $$$$ \\ $$$${in}\:{phase}\:\mathrm{1}\:{the}\:{reaction}\:{force}\:{N}\:{is} \\ $$$${always}\:{more}\:{than}\:{zero}\:{if}\:\lambda<\frac{\mathrm{2}}{\mathrm{3}}, \\ $$$${i}.{e}.\:{if}\:{b}<\frac{\mathrm{2}}{\mathrm{3}}{L}. \\ $$
