Question Number 30002 by rahul 19 last updated on 14/Feb/18
Commented by ajfour last updated on 14/Feb/18
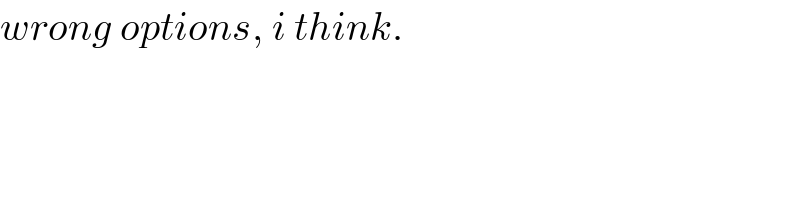
$${wrong}\:{options},\:{i}\:{think}. \\ $$
Commented by ajfour last updated on 15/Feb/18
Commented by ajfour last updated on 15/Feb/18
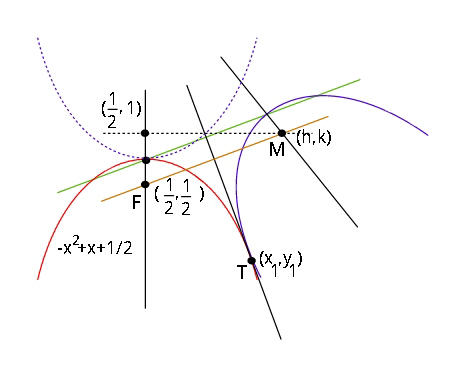
![let slope of common tangent be m. m=(dy/dx)∣_x_1 = −2x_1 +1 ...(i) y_1 =−x_1 ^2 +x_1 +(1/2) .....(ii) slope of FM=((k−(1/2))/(h−(1/2))) = −(1/m) ⇒ m=((2h−1)/(1−2k)) .....(iii) eq. of tangent y−y_1 =m(x−x_1 ) mid point of FM is (h+(1/2) , k+(1/2)) It lies on tangent, hence k+(1/2)−2y_1 =m(h+(1/2)−2x_1 ) ...(iv) using (i), (ii) and (iii) in (iv) : k+(1/2)+2x_1 ^2 −2x_1 −1= (1−2x_1 )(h+(1/2)−2x_1 ) k+(1/2)+2x_1 ^2 −2x_1 −1=h+(1/2)−2x_1 −2hx_1 −x_1 +4x_1 ^2 k−1=h(1−2x_1 )+2x_1 ^2 −x_1 k−1=(h−x_1 )(1−2x_1 ) k−1=(h−x_1 )m k−1=(h+((m−1)/2))m 2(k−1)=(2h−1+m)m 2(k−1)=(2h−1+((2h−1)/(1−2k)))(((2h−1)/(1−2k))) 2(k−1)=(((2h−1)^2 )/((1−2k)))(((2−2k)/(1−2k))) ⇒ (k−1)[1+(((2h−1)/(1−2k)))^2 ]=0 ⇒ k=1 hence locus is y=1 . (There has to be a shorter way, i couldn′t find presently)](https://www.tinkutara.com/question/Q30044.png)
$${let}\:{slope}\:{of}\:{common}\:{tangent}\:{be}\:\boldsymbol{{m}}. \\ $$$$\boldsymbol{{m}}=\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}\mid_{{x}_{\mathrm{1}} } \:=\:−\mathrm{2}{x}_{\mathrm{1}} +\mathrm{1}\:\:\:\:\:…\left({i}\right) \\ $$$${y}_{\mathrm{1}} =−{x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:…..\left({ii}\right) \\ $$$${slope}\:{of}\:{FM}=\frac{{k}−\frac{\mathrm{1}}{\mathrm{2}}}{{h}−\frac{\mathrm{1}}{\mathrm{2}}}\:=\:−\frac{\mathrm{1}}{{m}} \\ $$$$\Rightarrow\:\:{m}=\frac{\mathrm{2}{h}−\mathrm{1}}{\mathrm{1}−\mathrm{2}{k}}\:\:\:\:\:\:\:\:\:…..\left({iii}\right) \\ $$$${eq}.\:{of}\:{tangent}\: \\ $$$${y}−{y}_{\mathrm{1}} ={m}\left({x}−{x}_{\mathrm{1}} \right) \\ $$$${mid}\:{point}\:{of}\:{FM}\:{is}\:\left({h}+\frac{\mathrm{1}}{\mathrm{2}}\:,\:{k}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${It}\:{lies}\:{on}\:{tangent},\:{hence} \\ $$$${k}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}{y}_{\mathrm{1}} ={m}\left({h}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}{x}_{\mathrm{1}} \right)\:\:\:…\left({iv}\right) \\ $$$${using}\:\left({i}\right),\:\left({ii}\right)\:{and}\:\left({iii}\right)\:\:{in}\:\left({iv}\right)\:: \\ $$$${k}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}{x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{x}_{\mathrm{1}} −\mathrm{1}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}−\mathrm{2}{x}_{\mathrm{1}} \right)\left({h}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}{x}_{\mathrm{1}} \right) \\ $$$${k}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}{x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{x}_{\mathrm{1}} −\mathrm{1}={h}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}{x}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}{hx}_{\mathrm{1}} −{x}_{\mathrm{1}} +\mathrm{4}{x}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${k}−\mathrm{1}={h}\left(\mathrm{1}−\mathrm{2}{x}_{\mathrm{1}} \right)+\mathrm{2}{x}_{\mathrm{1}} ^{\mathrm{2}} −{x}_{\mathrm{1}} \\ $$$${k}−\mathrm{1}=\left({h}−{x}_{\mathrm{1}} \right)\left(\mathrm{1}−\mathrm{2}{x}_{\mathrm{1}} \right) \\ $$$${k}−\mathrm{1}=\left({h}−{x}_{\mathrm{1}} \right){m} \\ $$$${k}−\mathrm{1}=\left({h}+\frac{{m}−\mathrm{1}}{\mathrm{2}}\right){m} \\ $$$$\mathrm{2}\left({k}−\mathrm{1}\right)=\left(\mathrm{2}{h}−\mathrm{1}+{m}\right){m} \\ $$$$\mathrm{2}\left({k}−\mathrm{1}\right)=\left(\mathrm{2}{h}−\mathrm{1}+\frac{\mathrm{2}{h}−\mathrm{1}}{\mathrm{1}−\mathrm{2}{k}}\right)\left(\frac{\mathrm{2}{h}−\mathrm{1}}{\mathrm{1}−\mathrm{2}{k}}\right) \\ $$$$\mathrm{2}\left({k}−\mathrm{1}\right)=\frac{\left(\mathrm{2}{h}−\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{2}{k}\right)}\left(\frac{\mathrm{2}−\mathrm{2}{k}}{\mathrm{1}−\mathrm{2}{k}}\right) \\ $$$$\Rightarrow\:\:\left({k}−\mathrm{1}\right)\left[\mathrm{1}+\left(\frac{\mathrm{2}{h}−\mathrm{1}}{\mathrm{1}−\mathrm{2}{k}}\right)^{\mathrm{2}} \right]=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{k}=\mathrm{1} \\ $$$${hence}\:{locus}\:{is}\:\:\:\:\boldsymbol{{y}}=\mathrm{1}\:\:\:. \\ $$$$\left({There}\:{has}\:{to}\:{be}\:{a}\:{shorter}\:{way},\right. \\ $$$$\left.\:\:\:{i}\:{couldn}'{t}\:{find}\:{presently}\right) \\ $$
Commented by rahul 19 last updated on 15/Feb/18

$$\mathrm{thank}\:\mathrm{u}\:\mathrm{sir}! \\ $$$$\omega\boldsymbol{\mathrm{o}\omega}. \\ $$
Commented by rahul 19 last updated on 15/Feb/18

$$\mathrm{ok}\:\mathrm{sir},\:\mathrm{then}\:\mathrm{plz}\:\mathrm{provide}\:\mathrm{your}\:\mathrm{solution}. \\ $$$$\mathrm{ignoring}\:\mathrm{the}\:\mathrm{options}. \\ $$
