Question Number 30166 by Tinkutara last updated on 17/Feb/18
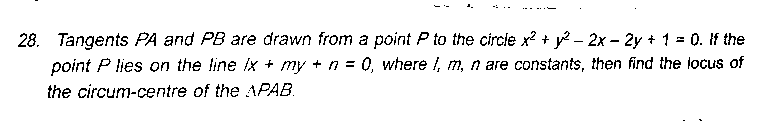
Commented by ajfour last updated on 18/Feb/18

Commented by ajfour last updated on 18/Feb/18

$${centre}\:{of}\:{circle}\:\:{Q}\left(\mathrm{1},\mathrm{1}\right) \\ $$$${point}\:{P}\:{of}\:{line}\:\left(\alpha,\beta\right) \\ $$$${let}\:{centre}\:{of}\:{circumcircle}\:{of} \\ $$$$\bigtriangleup{APB}\:\:{be}\:{C}\left({h},{k}\right). \\ $$$${C}\:{is}\:{midpoint}\:{of}\:{QP}. \\ $$$${so}\:\:\:\mathrm{2}{h}=\alpha+\mathrm{1}\:\:,\:\:\:\mathrm{2}{k}=\beta+\mathrm{1} \\ $$$${hence}\:\:\alpha\:=\:\mathrm{2}{h}−\mathrm{1}\:\:,\:\:\beta\:=\:\mathrm{2}{k}−\mathrm{1} \\ $$$${As}\:\:\left(\alpha,\:\beta\right)\:{lies}\:{on}\:{line}\:{lx}+{my}+{n}=\mathrm{0} \\ $$$${we}\:{have} \\ $$$$\:\:\:\:\:\:\:\:{l}\left(\mathrm{2}{h}−\mathrm{1}\right)+{m}\left(\mathrm{2}{k}−\mathrm{1}\right)+{n}=\mathrm{0} \\ $$$${hence}\:{required}\:{locus}\:{is} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}\boldsymbol{{lx}}+\mathrm{2}\boldsymbol{{my}}+\boldsymbol{{n}}\:=\:\boldsymbol{{l}}+\boldsymbol{{m}}\:. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 18/Feb/18
������ Thanks!
