Question Number 30256 by mondodotto@gmail.com last updated on 19/Feb/18
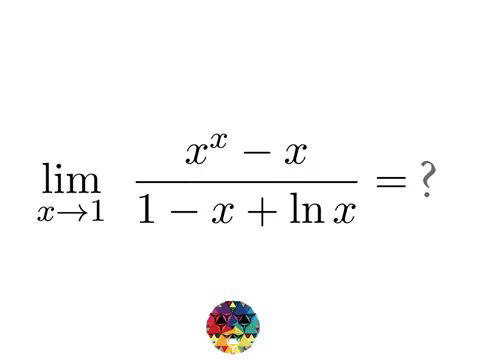
Commented by abdo imad last updated on 19/Feb/18

$${in}\:{this}\:{case}\:{is}\:{better}\:{to}\:{use}\:{hospital}\:{theorem}\:{let}\:{put} \\ $$$${u}\left({x}\right)={x}^{{x}} \:−{x}\:{and}\:{v}\left({x}\right)=\mathrm{1}−{x}\:+{lnx}\:{wehave}\:{u}\left(\mathrm{1}\right)={v}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${u}\left({x}\right)={e}^{{xlnx}} −{x}\Rightarrow{u}^{'} \left({x}\right)=\left(\mathrm{1}+{lnx}\right){e}^{{xlnx}} \:−\mathrm{1}\:{and} \\ $$$${u}^{''} \left({x}\right)=\frac{\mathrm{1}}{{x}}\:{e}^{{xlnx}} \:+\left(\mathrm{1}+{lnx}\right)\left(\mathrm{1}+{lnx}\right){e}^{{xlnx}} \\ $$$$=\frac{\mathrm{1}}{{x}}\:+\left(\mathrm{1}+{lnx}\right)^{\mathrm{2}} \:{e}^{{xlnx}} \:\:\Rightarrow\:{u}^{''} \left(\mathrm{1}\right)=\:\mathrm{2} \\ $$$${v}^{'} \left({x}\right)=\:−\mathrm{1}\:+\frac{\mathrm{1}}{{x}}\:\Rightarrow\:{v}^{''} \left({x}\right)=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\Rightarrow{v}^{''} \left(\mathrm{1}\right)=−\mathrm{1}\:{so} \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} \:\:\frac{{x}^{{x}} \:−{x}}{\mathrm{1}−{x}\:+{lnx}}\:=−\mathrm{2}\:. \\ $$
