Question Number 30355 by mondodotto@gmail.com last updated on 21/Feb/18
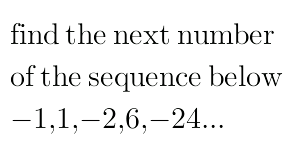
Answered by $@ty@m last updated on 21/Feb/18

$$\mathrm{120} \\ $$
Commented by mondodotto@gmail.com last updated on 21/Feb/18
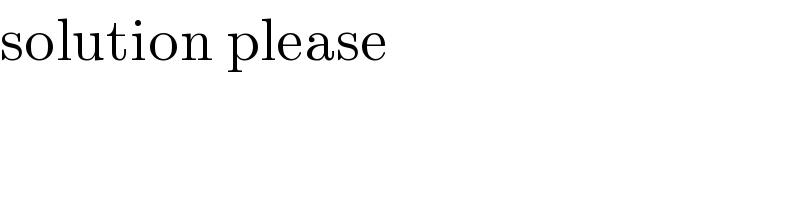
$$\mathrm{solution}\:\mathrm{please} \\ $$
Commented by MJS last updated on 21/Feb/18
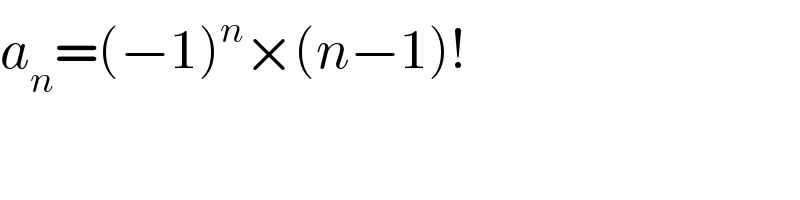
$${a}_{{n}} =\left(−\mathrm{1}\right)^{{n}} ×\left({n}−\mathrm{1}\right)! \\ $$
Answered by MJS last updated on 21/Feb/18
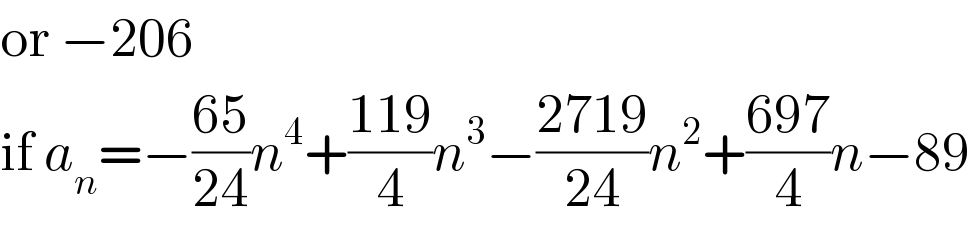
$$\mathrm{or}\:−\mathrm{206} \\ $$$$\mathrm{if}\:{a}_{{n}} =−\frac{\mathrm{65}}{\mathrm{24}}{n}^{\mathrm{4}} +\frac{\mathrm{119}}{\mathrm{4}}{n}^{\mathrm{3}} −\frac{\mathrm{2719}}{\mathrm{24}}{n}^{\mathrm{2}} +\frac{\mathrm{697}}{\mathrm{4}}{n}−\mathrm{89} \\ $$
Commented by mondodotto@gmail.com last updated on 21/Feb/18

$$\mathrm{more}\:\mathrm{explaination}\:\mathrm{please} \\ $$
Commented by MJS last updated on 21/Feb/18
![5 given points determine a polynome function P_1 = [(1),((−1)) ] P_2 = [(2),(1) ] P_3 = [(3),((−2)) ] P_4 = [(4),(6) ] P_5 = [(5),((−24)) ] P_n = [(x_n ),(y_n ) ] with y_n =ax_n ^4 +bx_n ^3 +cx_n ^2 +dx_n +e lead to a linear system which can be solved for {a, b, c, d, e}](https://www.tinkutara.com/question/Q30380.png)
$$\mathrm{5}\:\mathrm{given}\:\mathrm{points}\:\mathrm{determine}\:\mathrm{a} \\ $$$$\mathrm{polynome}\:\mathrm{function} \\ $$$${P}_{\mathrm{1}} =\begin{bmatrix}{\mathrm{1}}\\{−\mathrm{1}}\end{bmatrix}\:{P}_{\mathrm{2}} =\begin{bmatrix}{\mathrm{2}}\\{\mathrm{1}}\end{bmatrix}\:{P}_{\mathrm{3}} =\begin{bmatrix}{\mathrm{3}}\\{−\mathrm{2}}\end{bmatrix} \\ $$$${P}_{\mathrm{4}} =\begin{bmatrix}{\mathrm{4}}\\{\mathrm{6}}\end{bmatrix}\:{P}_{\mathrm{5}} =\begin{bmatrix}{\mathrm{5}}\\{−\mathrm{24}}\end{bmatrix} \\ $$$${P}_{{n}} =\begin{bmatrix}{{x}_{{n}} }\\{{y}_{{n}} }\end{bmatrix}\:\mathrm{with}\:{y}_{{n}} ={ax}_{{n}} ^{\mathrm{4}} +{bx}_{{n}} ^{\mathrm{3}} +{cx}_{{n}} ^{\mathrm{2}} +{dx}_{{n}} +{e} \\ $$$$\mathrm{lead}\:\mathrm{to}\:\mathrm{a}\:\mathrm{linear}\:\mathrm{system}\:\mathrm{which}\:\mathrm{can} \\ $$$$\mathrm{be}\:\mathrm{solved}\:\mathrm{for}\:\left\{{a},\:{b},\:{c},\:{d},\:{e}\right\} \\ $$
