Question Number 30615 by Tinkutara last updated on 23/Feb/18

Answered by ajfour last updated on 23/Feb/18
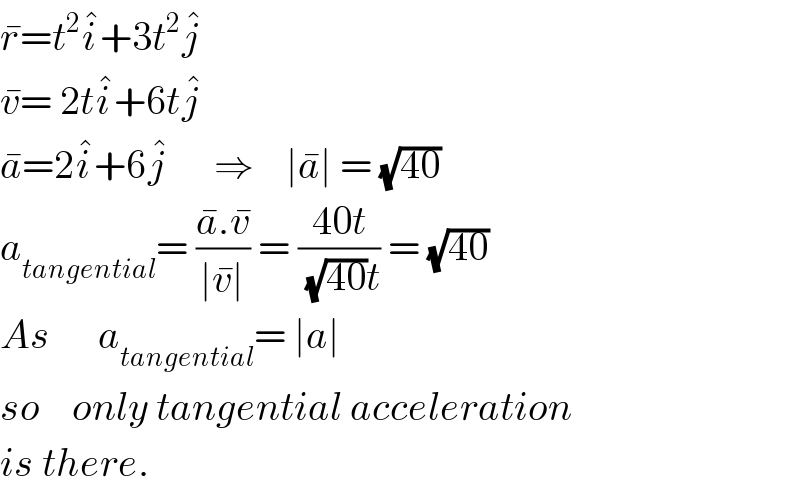
$$\bar {{r}}={t}^{\mathrm{2}} \hat {{i}}+\mathrm{3}{t}^{\mathrm{2}} \hat {{j}} \\ $$$$\bar {{v}}=\:\mathrm{2}{t}\hat {{i}}+\mathrm{6}{t}\hat {{j}} \\ $$$$\bar {{a}}=\mathrm{2}\hat {{i}}+\mathrm{6}\hat {{j}}\:\:\:\:\:\:\Rightarrow\:\:\:\:\mid\bar {{a}}\mid\:=\:\sqrt{\mathrm{40}} \\ $$$${a}_{{tangential}} =\:\frac{\bar {{a}}.\bar {{v}}}{\mid\bar {{v}}\mid}\:=\:\frac{\mathrm{40}{t}}{\:\sqrt{\mathrm{40}}{t}}\:=\:\sqrt{\mathrm{40}}\:\: \\ $$$${As}\:\:\:\:\:\:{a}_{{tangential}} =\:\mid{a}\mid\:\: \\ $$$${so}\:\:\:\:{only}\:{tangential}\:{acceleration} \\ $$$${is}\:{there}. \\ $$
Commented by Tinkutara last updated on 23/Feb/18
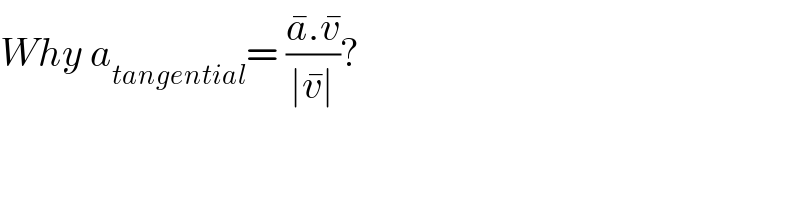
$${Why}\:{a}_{{tangential}} =\:\frac{\bar {{a}}.\bar {{v}}}{\mid\bar {{v}}\mid}? \\ $$
Commented by ajfour last updated on 23/Feb/18
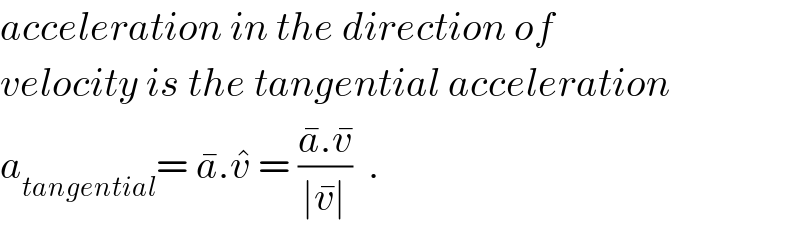
$${acceleration}\:{in}\:{the}\:{direction}\:{of} \\ $$$${velocity}\:{is}\:{the}\:{tangential}\:{acceleration} \\ $$$${a}_{{tangential}} =\:\bar {{a}}.\hat {{v}}\:=\:\frac{\bar {{a}}.\bar {{v}}}{\mid\bar {{v}}\mid}\:\:. \\ $$
Commented by Tinkutara last updated on 23/Feb/18
Thank you very much Sir! I got the answer.
