Question Number 30711 by mondodotto@gmail.com last updated on 24/Feb/18

Answered by mrW2 last updated on 24/Feb/18
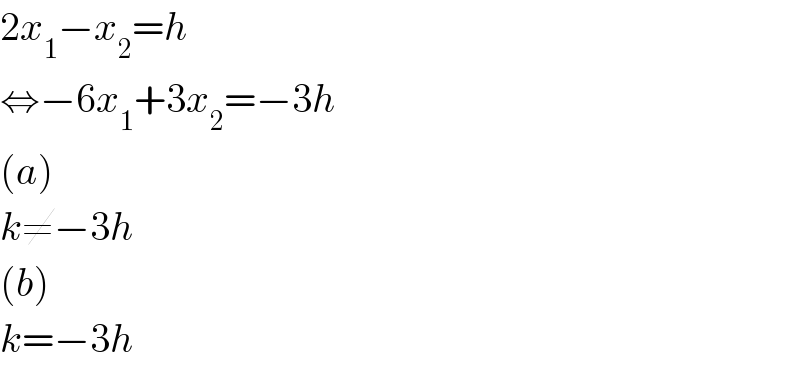
$$\mathrm{2}{x}_{\mathrm{1}} −{x}_{\mathrm{2}} ={h} \\ $$$$\Leftrightarrow−\mathrm{6}{x}_{\mathrm{1}} +\mathrm{3}{x}_{\mathrm{2}} =−\mathrm{3}{h} \\ $$$$\left({a}\right) \\ $$$${k}\neq−\mathrm{3}{h} \\ $$$$\left({b}\right) \\ $$$${k}=−\mathrm{3}{h} \\ $$
Commented by mrW2 last updated on 25/Feb/18

$${the}\:{eqn}.\:{system}\:{is} \\ $$$$−\mathrm{6}{x}_{\mathrm{1}} +\mathrm{3}{x}_{\mathrm{2}} =−\mathrm{3}{h} \\ $$$$−\mathrm{6}{x}_{\mathrm{1}} +\mathrm{3}{x}_{\mathrm{2}} ={k} \\ $$$${if}\:{k}\neq−\mathrm{3}{h}\:{the}\:{system}\:{will}\:{have}\:{no} \\ $$$${solution}. \\ $$$${if}\:{k}=−\mathrm{3}{h}\:{the}\:{system}\:{is}\:{in}\:{fact}\:{only} \\ $$$${one}\:{eqn}.\:−\mathrm{6}{x}_{\mathrm{1}} +\mathrm{3}{x}_{\mathrm{2}} ={k}\:{which}\:{infinite} \\ $$$${solutions}. \\ $$$${for}\:{both}\:{case}\:{there}\:{are}\:{infinite}\:{values} \\ $$$${for}\:{h}\:{and}\:{k}. \\ $$
Commented by mondodotto@gmail.com last updated on 25/Feb/18

$$\mathrm{more}\:\mathrm{explaination}\:\mathrm{please} \\ $$
Commented by mondodotto@gmail.com last updated on 25/Feb/18

$$\mathrm{we}'\mathrm{re}\:\mathrm{asked}\:\mathrm{to}\:\mathrm{find} \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{h}\:\mathrm{and}\:\mathrm{k} \\ $$
Commented by mondodotto@gmail.com last updated on 25/Feb/18
$$\mathrm{thanx}\:\mathrm{i}\:\mathrm{gat}\:\mathrm{you} \\ $$
