Menu Close

Question-30719

Tinku Tara 0 Comments
Pin




Question Number 30719 by mrW2 last updated on 24/Feb/18
Commented by mrW2 last updated on 25/Feb/18
This question is not visible any more. The question is: Find the side lengths of ΔPQR in terms of a,b,c.
$${This}\:{question}\:{is}\:{not}\:{visible}\:{any}\:{more}. \\ $$$${The}\:{question}\:{is}: \\ $$$${Find}\:{the}\:{side}\:{lengths}\:{of}\:\Delta{PQR}\:{in} \\ $$$${terms}\:{of}\:{a},{b},{c}. \\ $$
Commented by mrW2 last updated on 24/Feb/18
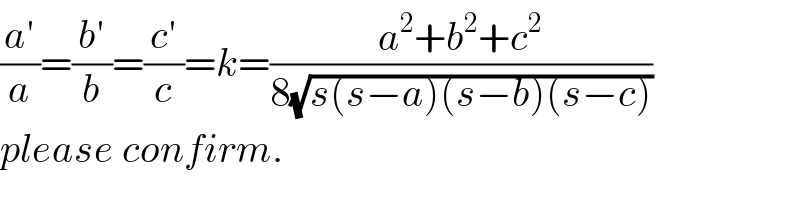
((a′)/a)=((b′)/b)=((c′)/c)=k=((a^2 +b^2 +c^2 )/(8(√(s(s−a)(s−b)(s−c))))) please confirm.
$$\frac{{a}'}{{a}}=\frac{{b}'}{{b}}=\frac{{c}'}{{c}}={k}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{8}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}} \\ $$$${please}\:{confirm}. \\ $$
Commented by ajfour last updated on 25/Feb/18
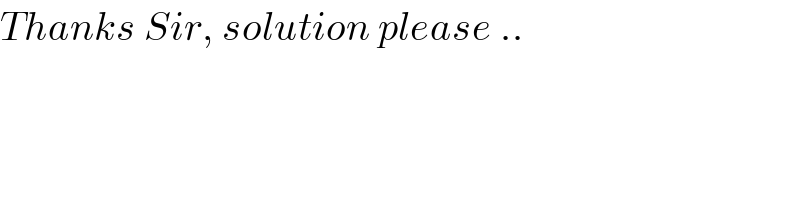
Thanks Sir, solution please ..
$${Thanks}\:{Sir},\:{solution}\:{please}\:.. \\ $$
Commented by beh.i83417@gmail.com last updated on 25/Feb/18
.
$$. \\ $$
Answered by mrW2 last updated on 25/Feb/18
Commented by mrW2 last updated on 25/Feb/18
a′=RP=RF+FG+GP RF=((IF)/(sin B))=((AF−AI)/(sin B))=(((c/2)−AE cos A)/(sin B))=((c−b cos A)/( 2sin B)) FG=BF sin B=((c sin B)/2) GP=((GD)/(tan C))=((BD−BG)/(tan C))=(((a/2)−BF cos B)/(tan C))=((a−c cos B)/(2 tan C)) ⇒a′=((c−b cos A)/( 2sin B))+((c sin B)/2)+((a−c cos B)/(2 tan C)) ⇒a′=(((c−b cos A)sin C+c sin^2 B sin C+(a−c cos B)sin B cos C)/(2 sin B sin C)) ⇒a′=((c sin C−b cos A sin C+c sin^2 B sin C+a sin B cos C−c cos B sin B cos C)/(2 sin B sin C)) ⇒a′=((c sin C−b cos A sin C+c sin B (sin B sin C−cos B cos C)+a sin B cos C)/(2 sin B sin C)) ⇒a′=((a sin B cos C−b cos A sin C+c (sin C+cos A sin B))/(2 sin B sin C)) (a/(sin A))=(b/(sin B))=(c/(sin C))=(1/λ)=2R=((abc)/(2(√(s(s−a)(a−b)(s−c))))) sin A=aλ, sin B=bλ, sin C=cλ ⇒a′=((ab cos C−bc cos A+c(c+b cos A))/(2bcλ)) ⇒a′=((ab cos C+c^2 )/(2bcλ)) ⇒a′=((((a^2 +b^2 −c^2 )/2)+c^2 )/(2bcλ)) ⇒a′=((a^2 +b^2 +c^2 )/(4bcλ)) ⇒a′=((a^2 +b^2 +c^2 )/(4bc×((2(√(s(s−a)(s−b)(s−c))))/(abc)))) ⇒a′=((a^2 +b^2 +c^2 )/((8(√(s(s−a)(s−b)(s−c))))/a)) ⇒a′=a×((a^2 +b^2 +c^2 )/(8(√(s(s−a)(s−b)(s−c))))) similarly: ⇒b′=b×((a^2 +b^2 +c^2 )/(8(√(s(s−a)(s−b)(s−c))))) ⇒c′=c×((a^2 +b^2 +c^2 )/(8(√(s(s−a)(s−b)(s−c)))))
$${a}'={RP}={RF}+{FG}+{GP} \\ $$$${RF}=\frac{{IF}}{\mathrm{sin}\:{B}}=\frac{{AF}−{AI}}{\mathrm{sin}\:{B}}=\frac{\frac{{c}}{\mathrm{2}}−{AE}\:\mathrm{cos}\:{A}}{\mathrm{sin}\:{B}}=\frac{{c}−{b}\:\mathrm{cos}\:{A}}{\:\mathrm{2sin}\:{B}} \\ $$$${FG}={BF}\:\mathrm{sin}\:{B}=\frac{{c}\:\mathrm{sin}\:{B}}{\mathrm{2}} \\ $$$${GP}=\frac{{GD}}{\mathrm{tan}\:{C}}=\frac{{BD}−{BG}}{\mathrm{tan}\:{C}}=\frac{\frac{{a}}{\mathrm{2}}−{BF}\:\mathrm{cos}\:{B}}{\mathrm{tan}\:{C}}=\frac{{a}−{c}\:\mathrm{cos}\:{B}}{\mathrm{2}\:\mathrm{tan}\:{C}} \\ $$$$ \\ $$$$\Rightarrow{a}'=\frac{{c}−{b}\:\mathrm{cos}\:{A}}{\:\mathrm{2sin}\:{B}}+\frac{{c}\:\mathrm{sin}\:{B}}{\mathrm{2}}+\frac{{a}−{c}\:\mathrm{cos}\:{B}}{\mathrm{2}\:\mathrm{tan}\:{C}} \\ $$$$\Rightarrow{a}'=\frac{\left({c}−{b}\:\mathrm{cos}\:{A}\right)\mathrm{sin}\:{C}+{c}\:\mathrm{sin}^{\mathrm{2}} \:{B}\:\mathrm{sin}\:{C}+\left({a}−{c}\:\mathrm{cos}\:{B}\right)\mathrm{sin}\:{B}\:\mathrm{cos}\:{C}}{\mathrm{2}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}} \\ $$$$\Rightarrow{a}'=\frac{{c}\:\mathrm{sin}\:{C}−{b}\:\mathrm{cos}\:{A}\:\mathrm{sin}\:{C}+{c}\:\mathrm{sin}^{\mathrm{2}} \:{B}\:\mathrm{sin}\:{C}+{a}\:\mathrm{sin}\:{B}\:\mathrm{cos}\:{C}−{c}\:\mathrm{cos}\:{B}\:\mathrm{sin}\:{B}\:\mathrm{cos}\:{C}}{\mathrm{2}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}} \\ $$$$\Rightarrow{a}'=\frac{{c}\:\mathrm{sin}\:{C}−{b}\:\mathrm{cos}\:{A}\:\mathrm{sin}\:{C}+{c}\:\mathrm{sin}\:{B}\:\left(\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}−\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\right)+{a}\:\mathrm{sin}\:{B}\:\mathrm{cos}\:{C}}{\mathrm{2}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}} \\ $$$$\Rightarrow{a}'=\frac{{a}\:\mathrm{sin}\:{B}\:\mathrm{cos}\:{C}−{b}\:\mathrm{cos}\:{A}\:\mathrm{sin}\:{C}+{c}\:\left(\mathrm{sin}\:{C}+\mathrm{cos}\:{A}\:\mathrm{sin}\:{B}\right)}{\mathrm{2}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}} \\ $$$$\frac{{a}}{\mathrm{sin}\:{A}}=\frac{{b}}{\mathrm{sin}\:{B}}=\frac{{c}}{\mathrm{sin}\:{C}}=\frac{\mathrm{1}}{\lambda}=\mathrm{2}{R}=\frac{{abc}}{\mathrm{2}\sqrt{{s}\left({s}−{a}\right)\left({a}−{b}\right)\left({s}−{c}\right)}} \\ $$$$\mathrm{sin}\:{A}={a}\lambda,\:\mathrm{sin}\:{B}={b}\lambda,\:\mathrm{sin}\:{C}={c}\lambda \\ $$$$\Rightarrow{a}'=\frac{{ab}\:\mathrm{cos}\:{C}−{bc}\:\mathrm{cos}\:{A}+{c}\left({c}+{b}\:\mathrm{cos}\:{A}\right)}{\mathrm{2}{bc}\lambda} \\ $$$$\Rightarrow{a}'=\frac{{ab}\:\mathrm{cos}\:{C}+{c}^{\mathrm{2}} }{\mathrm{2}{bc}\lambda} \\ $$$$\Rightarrow{a}'=\frac{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}}+{c}^{\mathrm{2}} }{\mathrm{2}{bc}\lambda} \\ $$$$\Rightarrow{a}'=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{4}{bc}\lambda} \\ $$$$\Rightarrow{a}'=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{4}{bc}×\frac{\mathrm{2}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}}{{abc}}} \\ $$$$\Rightarrow{a}'=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\frac{\mathrm{8}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}}{{a}}} \\ $$$$\Rightarrow{a}'={a}×\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{8}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}} \\ $$$${similarly}: \\ $$$$\Rightarrow{b}'={b}×\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{8}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}} \\ $$$$\Rightarrow{c}'={c}×\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{8}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}} \\ $$
Commented by ajfour last updated on 26/Feb/18
Thank you sir, great solution, and was much awaited !
$${Thank}\:{you}\:{sir},\:{great}\:{solution}, \\ $$$${and}\:{was}\:{much}\:{awaited}\:! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *