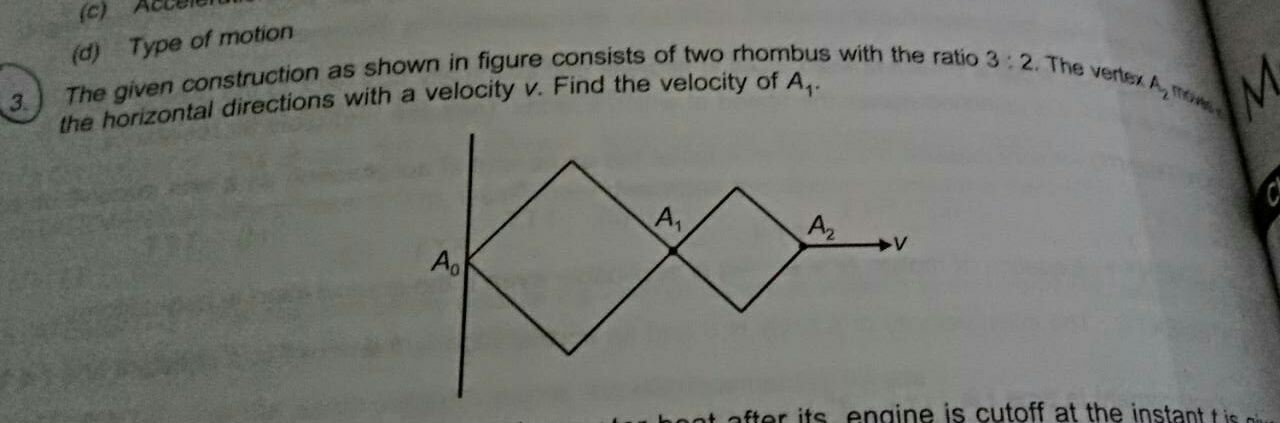
Question Number 30808 by 33 last updated on 26/Feb/18
Answered by mrW2 last updated on 26/Feb/18
Commented by mrW2 last updated on 26/Feb/18
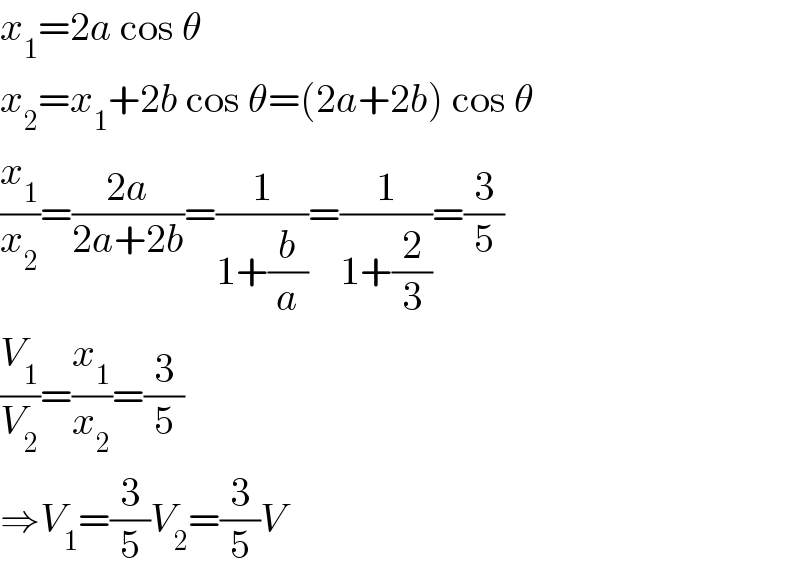
$${x}_{\mathrm{1}} =\mathrm{2}{a}\:\mathrm{cos}\:\theta \\ $$$${x}_{\mathrm{2}} ={x}_{\mathrm{1}} +\mathrm{2}{b}\:\mathrm{cos}\:\theta=\left(\mathrm{2}{a}+\mathrm{2}{b}\right)\:\mathrm{cos}\:\theta \\ $$$$\frac{{x}_{\mathrm{1}} }{{x}_{\mathrm{2}} }=\frac{\mathrm{2}{a}}{\mathrm{2}{a}+\mathrm{2}{b}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{{b}}{{a}}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\frac{{V}_{\mathrm{1}} }{{V}_{\mathrm{2}} }=\frac{{x}_{\mathrm{1}} }{{x}_{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\Rightarrow{V}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{5}}{V}_{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{5}}{V} \\ $$
Commented by 33 last updated on 26/Feb/18
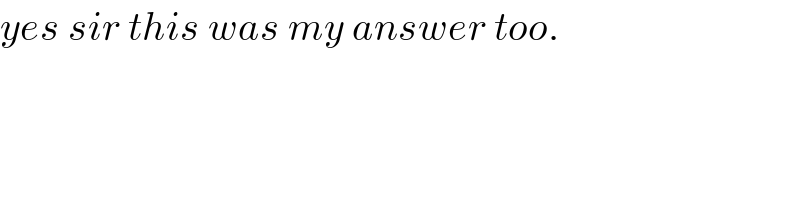
$${yes}\:{sir}\:{this}\:{was}\:{my}\:{answer}\:{too}. \\ $$
Commented by 33 last updated on 26/Feb/18
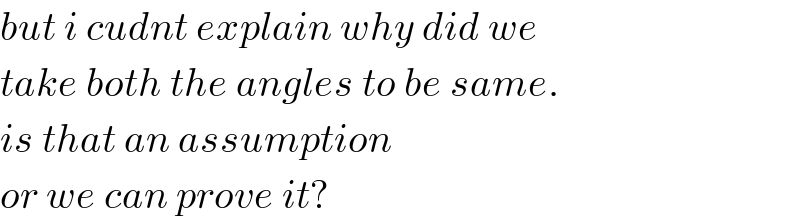
$${but}\:{i}\:{cudnt}\:{explain}\:{why}\:{did}\:{we} \\ $$$${take}\:{both}\:{the}\:{angles}\:{to}\:{be}\:{same}. \\ $$$${is}\:{that}\:{an}\:{assumption} \\ $$$${or}\:{we}\:{can}\:{prove}\:{it}? \\ $$
Commented by rahul 19 last updated on 26/Feb/18

$$\mathrm{why}\:{x}_{\mathrm{1}} =\:\mathrm{2}{acos}_{} \theta\:?\: \\ $$
Commented by mrW2 last updated on 26/Feb/18
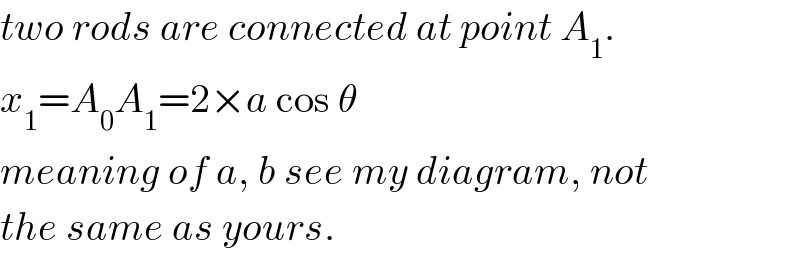
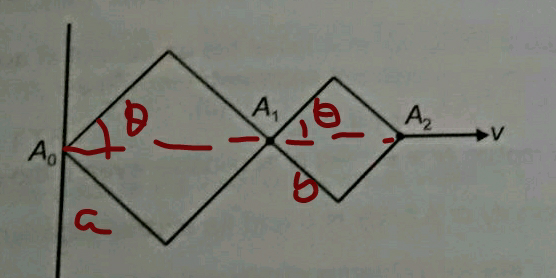
$${two}\:{rods}\:{are}\:{connected}\:{at}\:{point}\:{A}_{\mathrm{1}} . \\ $$$${x}_{\mathrm{1}} ={A}_{\mathrm{0}} {A}_{\mathrm{1}} =\mathrm{2}×{a}\:\mathrm{cos}\:\theta \\ $$$${meaning}\:{of}\:{a},\:{b}\:{see}\:{my}\:{diagram},\:{not} \\ $$$${the}\:{same}\:{as}\:{yours}. \\ $$
Commented by mrW2 last updated on 26/Feb/18

$${I}\:{said}\:{not}\:\mathrm{4}\:{but}\:\mathrm{2}\:{rods}\:{are}\:{connected} \\ $$$${at}\:{point}\:{A}_{\mathrm{1}} ,\:{therefore}\:{the}\:{angle}\:{is}\:{the} \\ $$$${same},\:{otherwise}\:{point}\:{A}_{\mathrm{1}} \:{has}\:{independent} \\ $$$${motion}\:{from}\:{point}\:{A}_{\mathrm{2}} . \\ $$
Commented by mrW2 last updated on 26/Feb/18

$${A}_{\mathrm{0}} \:{is}\:{fixed}\:{point},\:{A}_{\mathrm{1}} \:{is}\:{not}. \\ $$
Commented by rahul 19 last updated on 26/Feb/18

$$\mathrm{ok},\:\mathrm{thank}\:\mathrm{u}\:\mathrm{sir}. \\ $$
Commented by 33 last updated on 26/Feb/18
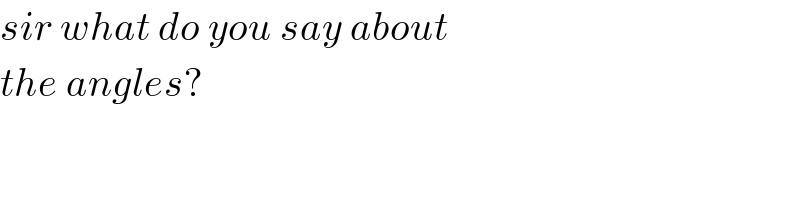
$${sir}\:{what}\:{do}\:{you}\:{say}\:{about} \\ $$$${the}\:{angles}? \\ $$
Commented by rahul 19 last updated on 26/Feb/18

$$\mathrm{ok},\:\mathrm{so}\:\mathrm{u}\:\mathrm{r}\:\mathrm{taking}\:\mathrm{distance}\:\mathrm{from}\:\mathrm{point}\:\mathrm{A}_{\mathrm{0}} . \\ $$$$\mathrm{what}\:\mathrm{if}\:\mathrm{i}\:\mathrm{take}\:\mathrm{reference}\:\mathrm{point}\:\mathrm{as}\:\mathrm{point}\:\mathrm{A}_{\mathrm{1}} \:? \\ $$
Commented by 33 last updated on 26/Feb/18
$${oh}\:{yes}\:{sir}.\:{got}\:{it}\:{thanks} \\ $$
Answered by 33 last updated on 26/Feb/18

Commented by rahul 19 last updated on 26/Feb/18
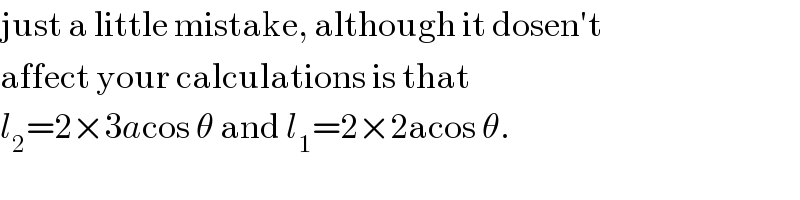
$$\mathrm{just}\:\mathrm{a}\:\mathrm{little}\:\mathrm{mistake},\:\mathrm{although}\:\mathrm{it}\:\mathrm{dosen}'\mathrm{t} \\ $$$$\mathrm{affect}\:\mathrm{your}\:\mathrm{calculations}\:\mathrm{is}\:\mathrm{that} \\ $$$${l}_{\mathrm{2}} =\mathrm{2}×\mathrm{3}{a}\mathrm{cos}\:\theta\:\mathrm{and}\:{l}_{\mathrm{1}} =\mathrm{2}×\mathrm{2acos}\:\theta. \\ $$
Answered by 33 last updated on 26/Feb/18

