Question Number 30820 by ajfour last updated on 26/Feb/18

Answered by mrW2 last updated on 26/Feb/18
![Eqn. of ellipse 1 (original one): (x^2 /a^2 )+(y^2 /b^2 )=1 ((r^2 cos^2 ϕ)/a^2 )+((r^2 sin^2 ϕ)/b^2 )=1 ⇒r^2 [((cos^2 ϕ)/a^2 )+((sin^2 ϕ)/b^2 )]=1 ⇒r^2 =((a^2 b^2 )/(a^2 sin^2 ϕ+b^2 cos^2 ϕ)) Eqn. of ellipse 2 (rotated one): ⇒r^2 [((cos^2 (ϕ−θ))/a^2 )+((sin^2 (ϕ−θ))/b^2 )]=1 ⇒r^2 =((a^2 b^2 )/(a^2 sin^2 (ϕ−θ)+b^2 cos^2 (ϕ−θ))) Intersection of both ellipses: ((cos^2 ϕ)/a^2 )+((sin^2 ϕ)/b^2 )=((cos^2 (ϕ−θ))/a^2 )+((sin^2 (ϕ−θ))/b^2 ) b^2 cos^2 ϕ+a^2 sin^2 ϕ=b^2 cos^2 (ϕ−θ)+a^2 sin^2 (ϕ−θ) b^2 cos^2 ϕ+a^2 sin^2 ϕ=b^2 (cos ϕ cos θ+sin ϕ sin θ)^2 +a^2 (sin ϕ cos θ−cos ϕ sin θ)^2 b^2 cos^2 ϕ+a^2 sin^2 ϕ=b^2 cos^2 ϕ cos^2 θ+b^2 sin^2 ϕ sin^2 θ+2b^2 sin ϕ cos ϕ sin θ cos θ+a^2 sin^2 ϕ cos^2 θ+a^2 cos^2 ϕ sin^2 θ−2a^2 sin ϕ cos ϕ sin θ cos θ b^2 (cos^2 ϕ−sin^2 ϕ) sin^2 θ−a^2 (cos^2 ϕ−sin^2 ϕ) sin^2 θ=2(b^2 −a^2 ) sin ϕ cos ϕ sin θ cos θ (b^2 −a^2 )cos 2ϕ sin^2 θ=(b^2 −a^2 ) sin 2ϕ sin θ cos θ cos 2ϕ sin θ= sin 2ϕ cos θ ⇒tan 2ϕ=tan θ ⇒2ϕ=θ or θ+π ⇒ϕ_1 =(θ/2) ⇒ϕ_2 =(θ/2)+(π/2) A=∫_ϕ_1 ^( ϕ_2 ) ∫_r_1 ^r_2 rdrdϕ =(1/2)∫_ϕ_1 ^( ϕ_2 ) [r_2 ^2 −r_1 ^2 ]dϕ =((a^2 b^2 )/2)∫_ϕ_1 ^( ϕ_2 ) [(1/(a^2 sin^2 (ϕ−θ)+b^2 cos^2 (ϕ−θ)))−(1/(a^2 sin^2 ϕ+b^2 cos^2 ϕ))]dϕ =((a^2 b^2 )/2)[(1/(ab))tan^(−1) {(a/b) tan (ϕ−θ)}−(1/(ab))tan^(−1) {(a/b) tan ϕ}]_ϕ_1 ^ϕ_2 =((ab)/2)[tan^(−1) {(a/b) tan (ϕ−θ)}−tan^(−1) {(a/b) tan ϕ}]_ϕ_1 ^ϕ_2 =((ab)/2)[tan^(−1) {(a/b) tan ((π/2)−(θ/2))}−tan^(−1) {(a/b) tan ((π/2)+(θ/2))}−tan^(−1) {(a/b) tan ((θ/2)−θ)}+tan^(−1) {(a/b) tan (θ/2)}] =((ab)/2)[2 tan^(−1) {(a/b) tan ((π/2)−(θ/2))}−π+2 tan^(−1) {(a/b) tan (θ/2)}] =ab[tan^(−1) {(a/b) tan ((π/2)−(θ/2))}+tan^(−1) {(a/b) tan (θ/2)}−(π/2)] =ab{(π/2)− tan^(−1) [((2ab)/((a^2 −b^2 )sin θ))]} ⇒A=ab tan^(−1) ∣(((a^2 −b^2 )sin θ)/(2ab))∣ An other way: A=(1/2)(πab−4∫_ϕ_1 ^( ϕ_2 ) (r_1 ^2 /2)dϕ) =ab(π/2)−∫_ϕ_1 ^( ϕ_2 ) ((a^2 b^2 )/(a^2 sin^2 ϕ+b^2 cos^2 ϕ))dϕ =ab(π/2)−a^2 b^2 [(1/(ab)) tan^(−1) {(a/b)tan ϕ}]_ϕ_1 ^ϕ_2 =ab(π/2)−ab[tan^(−1) {(a/b)tan ((π/2)+(θ/2))}−tan^(−1) {(a/b)tan ((θ/2))}] =ab(π/2)−ab[π−tan^(−1) {(a/b)tan ((π/2)−(θ/2))}−tan^(−1) {(a/b)tan ((θ/2))}] =ab[tan^(−1) {(a/b)tan ((π/2)−(θ/2))}+tan^(−1) {(a/b)tan ((θ/2))}−(π/2)] ..... as above](https://www.tinkutara.com/question/Q30824.png)
$${Eqn}.\:{of}\:{ellipse}\:\mathrm{1}\:\left({original}\:{one}\right): \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\varphi}{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\varphi}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{r}^{\mathrm{2}} \left[\frac{\mathrm{cos}^{\mathrm{2}} \:\varphi}{{a}^{\mathrm{2}} }+\frac{\mathrm{sin}^{\mathrm{2}} \:\varphi}{{b}^{\mathrm{2}} }\right]=\mathrm{1} \\ $$$$\Rightarrow{r}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\varphi+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\varphi} \\ $$$${Eqn}.\:{of}\:{ellipse}\:\mathrm{2}\:\left({rotated}\:{one}\right): \\ $$$$\Rightarrow{r}^{\mathrm{2}} \left[\frac{\mathrm{cos}^{\mathrm{2}} \:\left(\varphi−\theta\right)}{{a}^{\mathrm{2}} }+\frac{\mathrm{sin}^{\mathrm{2}} \:\left(\varphi−\theta\right)}{{b}^{\mathrm{2}} }\right]=\mathrm{1} \\ $$$$\Rightarrow{r}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\left(\varphi−\theta\right)+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\left(\varphi−\theta\right)} \\ $$$$ \\ $$$${Intersection}\:{of}\:{both}\:{ellipses}: \\ $$$$\frac{\mathrm{cos}^{\mathrm{2}} \:\varphi}{{a}^{\mathrm{2}} }+\frac{\mathrm{sin}^{\mathrm{2}} \:\varphi}{{b}^{\mathrm{2}} }=\frac{\mathrm{cos}^{\mathrm{2}} \:\left(\varphi−\theta\right)}{{a}^{\mathrm{2}} }+\frac{\mathrm{sin}^{\mathrm{2}} \:\left(\varphi−\theta\right)}{{b}^{\mathrm{2}} } \\ $$$${b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\varphi+{a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\varphi={b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\left(\varphi−\theta\right)+{a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\left(\varphi−\theta\right) \\ $$$${b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\varphi+{a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\varphi={b}^{\mathrm{2}} \:\left(\mathrm{cos}\:\varphi\:\mathrm{cos}\:\theta+\mathrm{sin}\:\varphi\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \:\left(\mathrm{sin}\:\varphi\:\mathrm{cos}\:\theta−\mathrm{cos}\:\varphi\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\varphi+{a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\varphi={b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\varphi\:\mathrm{cos}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\varphi\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}{b}^{\mathrm{2}} \:\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta+{a}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\varphi\:\mathrm{cos}^{\mathrm{2}} \:\theta+{a}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\varphi\:\mathrm{sin}^{\mathrm{2}} \:\theta−\mathrm{2}{a}^{\mathrm{2}} \:\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta \\ $$$${b}^{\mathrm{2}} \:\left(\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{sin}^{\mathrm{2}} \:\varphi\right)\:\mathrm{sin}^{\mathrm{2}} \:\theta−{a}^{\mathrm{2}} \:\left(\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{sin}^{\mathrm{2}} \:\varphi\right)\:\mathrm{sin}^{\mathrm{2}} \:\theta=\mathrm{2}\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:\mathrm{sin}\:\varphi\:\mathrm{cos}\:\varphi\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta \\ $$$$\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\mathrm{cos}\:\mathrm{2}\varphi\:\mathrm{sin}^{\mathrm{2}} \:\theta=\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:\mathrm{sin}\:\mathrm{2}\varphi\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta \\ $$$$\mathrm{cos}\:\mathrm{2}\varphi\:\mathrm{sin}\:\theta=\:\mathrm{sin}\:\mathrm{2}\varphi\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{2}\varphi=\mathrm{tan}\:\theta \\ $$$$\Rightarrow\mathrm{2}\varphi=\theta\:{or}\:\theta+\pi \\ $$$$\Rightarrow\varphi_{\mathrm{1}} =\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\varphi_{\mathrm{2}} =\frac{\theta}{\mathrm{2}}+\frac{\pi}{\mathrm{2}} \\ $$$${A}=\int_{\varphi_{\mathrm{1}} } ^{\:\varphi_{\mathrm{2}} } \int_{{r}_{\mathrm{1}} } ^{{r}_{\mathrm{2}} } {rdrd}\varphi \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\varphi_{\mathrm{1}} } ^{\:\varphi_{\mathrm{2}} } \left[{r}_{\mathrm{2}} ^{\mathrm{2}} −{r}_{\mathrm{1}} ^{\mathrm{2}} \right]{d}\varphi \\ $$$$=\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\mathrm{2}}\int_{\varphi_{\mathrm{1}} } ^{\:\varphi_{\mathrm{2}} } \left[\frac{\mathrm{1}}{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\left(\varphi−\theta\right)+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\left(\varphi−\theta\right)}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\varphi+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\varphi}\right]{d}\varphi \\ $$$$=\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\mathrm{1}}{{ab}}\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\left(\varphi−\theta\right)\right\}−\frac{\mathrm{1}}{{ab}}\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\varphi\right\}\right]_{\varphi_{\mathrm{1}} } ^{\varphi_{\mathrm{2}} } \\ $$$$=\frac{{ab}}{\mathrm{2}}\left[\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\left(\varphi−\theta\right)\right\}−\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\varphi\right\}\right]_{\varphi_{\mathrm{1}} } ^{\varphi_{\mathrm{2}} } \\ $$$$=\frac{{ab}}{\mathrm{2}}\left[\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}}\right)\right\}−\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}+\frac{\theta}{\mathrm{2}}\right)\right\}−\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\left(\frac{\theta}{\mathrm{2}}−\theta\right)\right\}+\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right\}\right] \\ $$$$=\frac{{ab}}{\mathrm{2}}\left[\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}}\right)\right\}−\pi+\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right\}\right] \\ $$$$={ab}\left[\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}}\right)\right\}+\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right\}−\frac{\pi}{\mathrm{2}}\right] \\ $$$$={ab}\left\{\frac{\pi}{\mathrm{2}}−\:\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{2}{ab}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:\theta}\right]\right\} \\ $$$$\Rightarrow{A}={ab}\:\mathrm{tan}^{−\mathrm{1}} \mid\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:\theta}{\mathrm{2}{ab}}\mid \\ $$$$ \\ $$$${An}\:{other}\:{way}: \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\left(\pi{ab}−\mathrm{4}\int_{\varphi_{\mathrm{1}} } ^{\:\varphi_{\mathrm{2}} } \frac{{r}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}}{d}\varphi\right) \\ $$$$={ab}\frac{\pi}{\mathrm{2}}−\int_{\varphi_{\mathrm{1}} } ^{\:\varphi_{\mathrm{2}} } \frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\varphi+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\varphi}{d}\varphi \\ $$$$={ab}\frac{\pi}{\mathrm{2}}−{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left[\frac{\mathrm{1}}{{ab}}\:\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\mathrm{tan}\:\varphi\right\}\right]_{\varphi_{\mathrm{1}} } ^{\varphi_{\mathrm{2}} } \\ $$$$={ab}\frac{\pi}{\mathrm{2}}−{ab}\left[\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}+\frac{\theta}{\mathrm{2}}\right)\right\}−\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\mathrm{tan}\:\left(\frac{\theta}{\mathrm{2}}\right)\right\}\right] \\ $$$$={ab}\frac{\pi}{\mathrm{2}}−{ab}\left[\pi−\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}}\right)\right\}−\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\mathrm{tan}\:\left(\frac{\theta}{\mathrm{2}}\right)\right\}\right] \\ $$$$={ab}\left[\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}}\right)\right\}+\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{a}}{{b}}\mathrm{tan}\:\left(\frac{\theta}{\mathrm{2}}\right)\right\}−\frac{\pi}{\mathrm{2}}\right] \\ $$$$…..\:{as}\:{above} \\ $$
Commented by ajfour last updated on 26/Feb/18
$${O}'\:\mathscr{MY}\:\:{God}!\:{You}\:{make}\:{it}\:{possible} \\ $$$${Sir}.{Thank}\:{you}\:{immensely}. \\ $$$${Its}\:{really}\:{great},\:{Sir}. \\ $$
Commented by ajfour last updated on 26/Feb/18
$${Yes}\:{Sir},\:{thank}\:{you}\:{again}. \\ $$
Commented by mrW2 last updated on 26/Feb/18
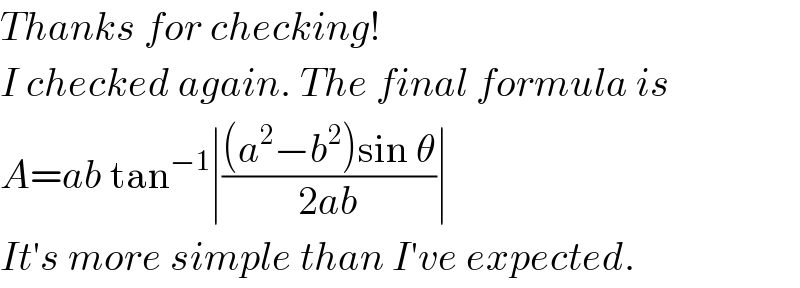
$${Thanks}\:{for}\:{checking}! \\ $$$${I}\:{checked}\:{again}.\:{The}\:{final}\:{formula}\:{is} \\ $$$${A}={ab}\:\mathrm{tan}^{−\mathrm{1}} \mid\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:\theta}{\mathrm{2}{ab}}\mid \\ $$$${It}'{s}\:{more}\:{simple}\:{than}\:{I}'{ve}\:{expected}. \\ $$
