Question Number 30916 by Tinkutara last updated on 28/Feb/18
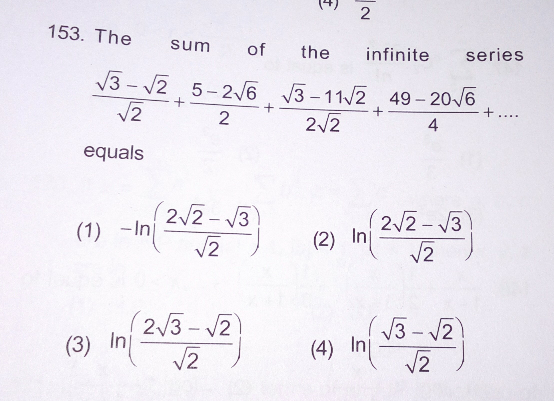
Commented by Tinkutara last updated on 28/Feb/18
Answer is 1⃣
Answered by $@ty@m last updated on 28/Feb/18
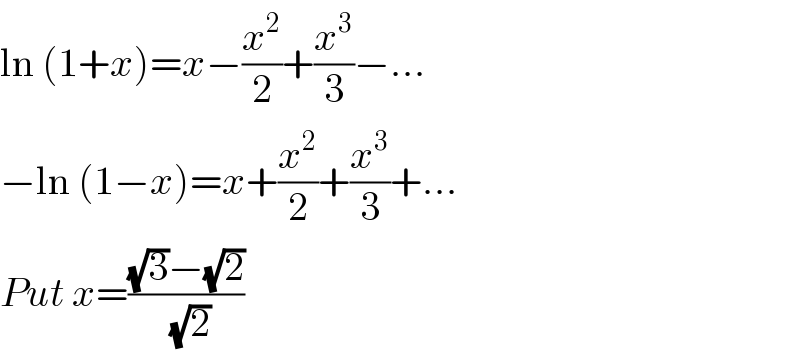
$$\mathrm{ln}\:\left(\mathrm{1}+{x}\right)={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−… \\ $$$$−\mathrm{ln}\:\left(\mathrm{1}−{x}\right)={x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+… \\ $$$${Put}\:{x}=\frac{\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by Tinkutara last updated on 01/Mar/18
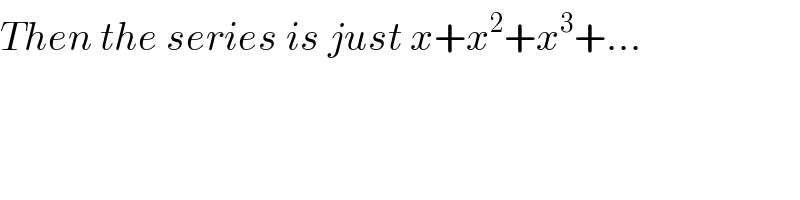
$${Then}\:{the}\:{series}\:{is}\:{just}\:{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +… \\ $$
Commented by $@ty@m last updated on 01/Mar/18
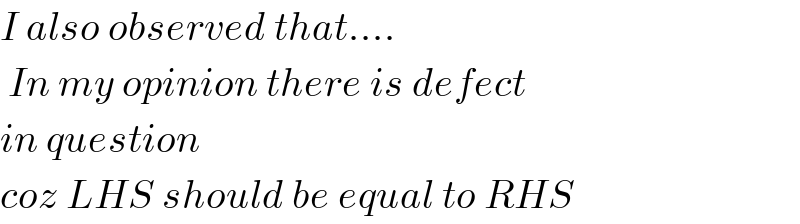
$${I}\:{also}\:{observed}\:{that}…. \\ $$$$\:{In}\:{my}\:{opinion}\:{there}\:{is}\:{defect} \\ $$$${in}\:{question} \\ $$$${coz}\:{LHS}\:{should}\:{be}\:{equal}\:{to}\:{RHS} \\ $$
Commented by Tinkutara last updated on 01/Mar/18
Question wrong surely?
