Menu Close

Question-30918

Tinku Tara 0 Comments
Pin




Question Number 30918 by naka3546 last updated on 28/Feb/18
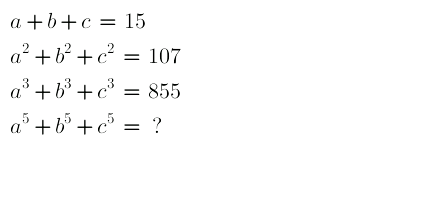
Answered by ajfour last updated on 28/Feb/18
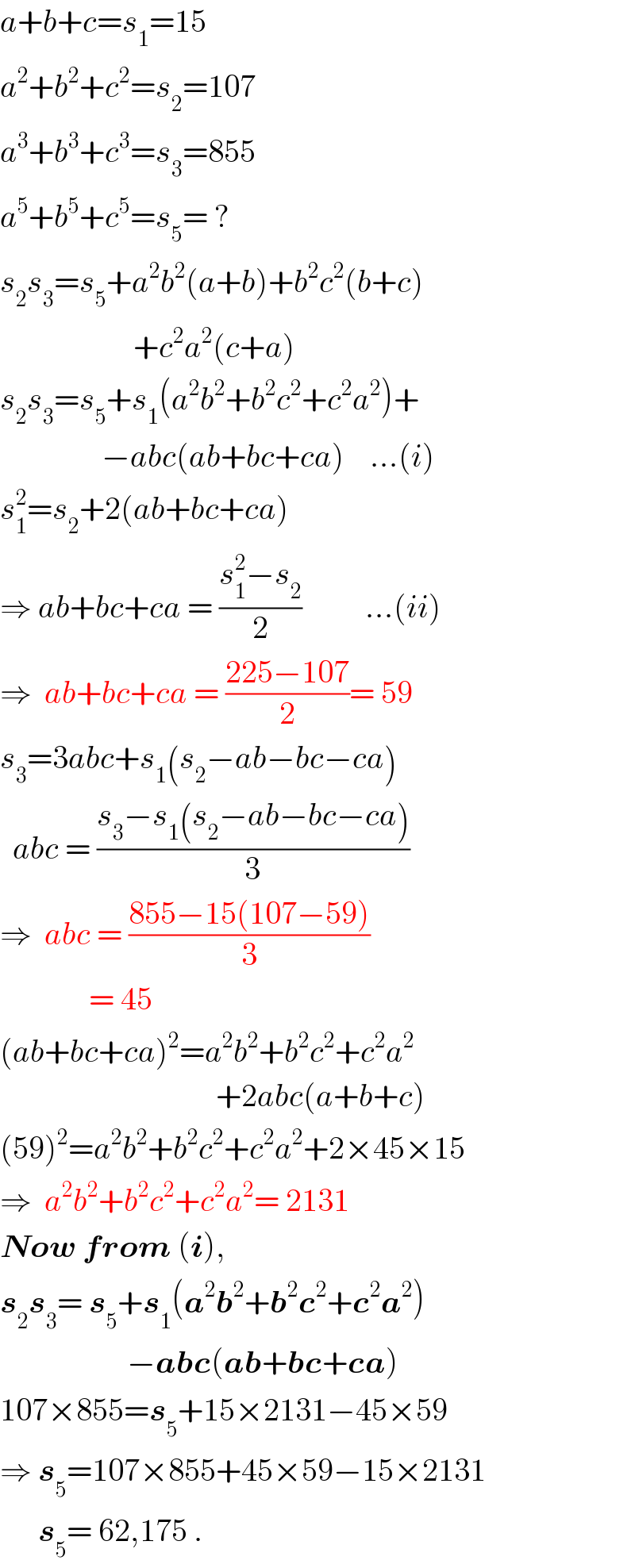
a+b+c=s_1 =15 a^2 +b^2 +c^2 =s_2 =107 a^3 +b^3 +c^3 =s_3 =855 a^5 +b^5 +c^5 =s_5 = ? s_2 s_3 =s_5 +a^2 b^2 (a+b)+b^2 c^2 (b+c) +c^2 a^2 (c+a) s_2 s_3 =s_5 +s_1 (a^2 b^2 +b^2 c^2 +c^2 a^2 )+ −abc(ab+bc+ca) ...(i) s_1 ^2 =s_2 +2(ab+bc+ca) ⇒ ab+bc+ca = ((s_1 ^2 −s_2 )/2) ...(ii) ⇒ ab+bc+ca = ((225−107)/2)= 59 s_3 =3abc+s_1 (s_2 −ab−bc−ca) abc = ((s_3 −s_1 (s_2 −ab−bc−ca))/3) ⇒ abc = ((855−15(107−59))/3) = 45 (ab+bc+ca)^2 =a^2 b^2 +b^2 c^2 +c^2 a^2 +2abc(a+b+c) (59)^2 =a^2 b^2 +b^2 c^2 +c^2 a^2 +2×45×15 ⇒ a^2 b^2 +b^2 c^2 +c^2 a^2 = 2131 Now from (i), s_2 s_3 = s_5 +s_1 (a^2 b^2 +b^2 c^2 +c^2 a^2 ) −abc(ab+bc+ca) 107×855=s_5 +15×2131−45×59 ⇒ s_5 =107×855+45×59−15×2131 s_5 = 62,175 .
$${a}+{b}+{c}={s}_{\mathrm{1}} =\mathrm{15} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} ={s}_{\mathrm{2}} =\mathrm{107} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} ={s}_{\mathrm{3}} =\mathrm{855} \\ $$$${a}^{\mathrm{5}} +{b}^{\mathrm{5}} +{c}^{\mathrm{5}} ={s}_{\mathrm{5}} =\:? \\ $$$${s}_{\mathrm{2}} {s}_{\mathrm{3}} ={s}_{\mathrm{5}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}+{b}\right)+{b}^{\mathrm{2}} {c}^{\mathrm{2}} \left({b}+{c}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{c}^{\mathrm{2}} {a}^{\mathrm{2}} \left({c}+{a}\right) \\ $$$${s}_{\mathrm{2}} {s}_{\mathrm{3}} ={s}_{\mathrm{5}} +{s}_{\mathrm{1}} \left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{abc}\left({ab}+{bc}+{ca}\right)\:\:\:\:…\left({i}\right) \\ $$$${s}_{\mathrm{1}} ^{\mathrm{2}} ={s}_{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$$\Rightarrow\:{ab}+{bc}+{ca}\:=\:\frac{{s}_{\mathrm{1}} ^{\mathrm{2}} −{s}_{\mathrm{2}} }{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\:\:{ab}+{bc}+{ca}\:=\:\frac{\mathrm{225}−\mathrm{107}}{\mathrm{2}}=\:\mathrm{59} \\ $$$${s}_{\mathrm{3}} =\mathrm{3}{abc}+{s}_{\mathrm{1}} \left({s}_{\mathrm{2}} −{ab}−{bc}−{ca}\right) \\ $$$$\:\:{abc}\:=\:\frac{{s}_{\mathrm{3}} −{s}_{\mathrm{1}} \left({s}_{\mathrm{2}} −{ab}−{bc}−{ca}\right)}{\mathrm{3}} \\ $$$$\Rightarrow\:\:{abc}\:=\:\frac{\mathrm{855}−\mathrm{15}\left(\mathrm{107}−\mathrm{59}\right)}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{45} \\ $$$$\left({ab}+{bc}+{ca}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}{abc}\left({a}+{b}+{c}\right) \\ $$$$\left(\mathrm{59}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} +\mathrm{2}×\mathrm{45}×\mathrm{15} \\ $$$$\Rightarrow\:\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} =\:\mathrm{2131} \\ $$$$\boldsymbol{{Now}}\:\boldsymbol{{from}}\:\left(\boldsymbol{{i}}\right), \\ $$$$\boldsymbol{{s}}_{\mathrm{2}} \boldsymbol{{s}}_{\mathrm{3}} =\:\boldsymbol{{s}}_{\mathrm{5}} +\boldsymbol{{s}}_{\mathrm{1}} \left(\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{c}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} \boldsymbol{{a}}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\boldsymbol{{abc}}\left(\boldsymbol{{ab}}+\boldsymbol{{bc}}+\boldsymbol{{ca}}\right) \\ $$$$\mathrm{107}×\mathrm{855}=\boldsymbol{{s}}_{\mathrm{5}} +\mathrm{15}×\mathrm{2131}−\mathrm{45}×\mathrm{59} \\ $$$$\Rightarrow\:\boldsymbol{{s}}_{\mathrm{5}} =\mathrm{107}×\mathrm{855}+\mathrm{45}×\mathrm{59}−\mathrm{15}×\mathrm{2131} \\ $$$$\:\:\:\:\:\:\boldsymbol{{s}}_{\mathrm{5}} =\:\mathrm{62},\mathrm{175}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *