Question Number 30958 by rahul 19 last updated on 01/Mar/18
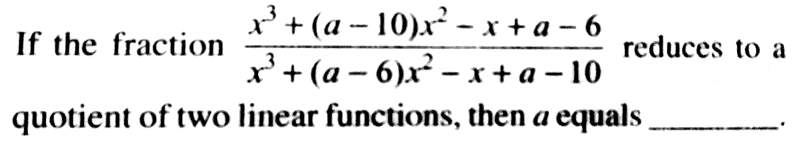
Commented by rahul 19 last updated on 01/Mar/18

Commented by rahul 19 last updated on 01/Mar/18
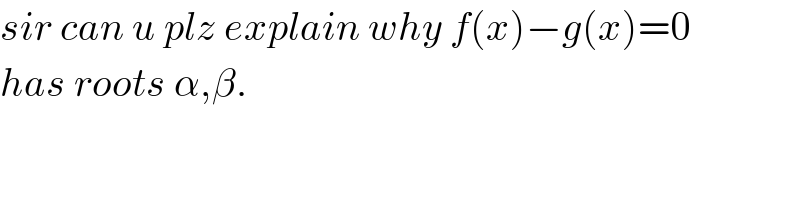
$${sir}\:{can}\:{u}\:{plz}\:{explain}\:{why}\:{f}\left({x}\right)−{g}\left({x}\right)=\mathrm{0} \\ $$$${has}\:{roots}\:\alpha,\beta. \\ $$
Commented by ajfour last updated on 01/Mar/18
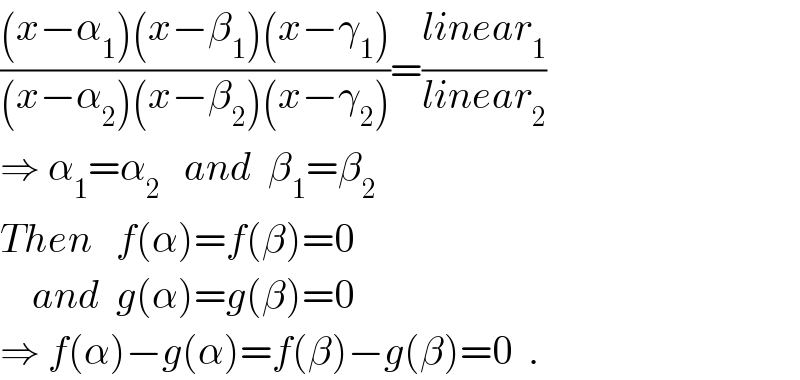
$$\frac{\left({x}−\alpha_{\mathrm{1}} \right)\left({x}−\beta_{\mathrm{1}} \right)\left({x}−\gamma_{\mathrm{1}} \right)}{\left({x}−\alpha_{\mathrm{2}} \right)\left({x}−\beta_{\mathrm{2}} \right)\left({x}−\gamma_{\mathrm{2}} \right)}=\frac{{linear}_{\mathrm{1}} }{{linear}_{\mathrm{2}} }\: \\ $$$$\Rightarrow\:\alpha_{\mathrm{1}} =\alpha_{\mathrm{2}} \:\:\:{and}\:\:\beta_{\mathrm{1}} =\beta_{\mathrm{2}} \\ $$$${Then}\:\:\:{f}\left(\alpha\right)={f}\left(\beta\right)=\mathrm{0} \\ $$$$\:\:\:\:{and}\:\:{g}\left(\alpha\right)={g}\left(\beta\right)=\mathrm{0} \\ $$$$\Rightarrow\:{f}\left(\alpha\right)−{g}\left(\alpha\right)={f}\left(\beta\right)−{g}\left(\beta\right)=\mathrm{0}\:\:. \\ $$
Commented by rahul 19 last updated on 01/Mar/18

$$\mathrm{now}\:\mathrm{it}'{s}\:{clear}\:\::{D}\: \\ $$
Answered by ajfour last updated on 01/Mar/18
![((x^3 +(a−10)x^2 −x+a−6)/(x^3 +(a−6)x^2 −x+a−10)) =((x+b)/(x+c)) ⇒ x^4 +(a−10+c)x^3 +[c(a−10)−1]x^2 +(a−6−c)x +c(a−6) = x^4 +(a−6+b)x^3 +[b(a−6)−1]x^2 + +(a−10−b)x+b(a−10) c(a−10)−1 = b(a−6)−1 ...(i) c(a−6)=b(a−10) ...(ii) ⇒ ((a−10)/(a−6))=((a−6)/(a−10)) or (a−10)^2 = (a−6)^2 −20a+100 = −12a+36 ⇒ a = 8 .](https://www.tinkutara.com/question/Q30962.png)
$$\frac{{x}^{\mathrm{3}} +\left({a}−\mathrm{10}\right){x}^{\mathrm{2}} −{x}+{a}−\mathrm{6}}{{x}^{\mathrm{3}} +\left({a}−\mathrm{6}\right){x}^{\mathrm{2}} −{x}+{a}−\mathrm{10}} \\ $$$$=\frac{{x}+{b}}{{x}+{c}} \\ $$$$\Rightarrow\:{x}^{\mathrm{4}} +\left({a}−\mathrm{10}+{c}\right){x}^{\mathrm{3}} +\left[{c}\left({a}−\mathrm{10}\right)−\mathrm{1}\right]{x}^{\mathrm{2}} +\left({a}−\mathrm{6}−{c}\right){x} \\ $$$$\:\:\:\:\:+{c}\left({a}−\mathrm{6}\right)\:=\:{x}^{\mathrm{4}} +\left({a}−\mathrm{6}+{b}\right){x}^{\mathrm{3}} +\left[{b}\left({a}−\mathrm{6}\right)−\mathrm{1}\right]{x}^{\mathrm{2}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({a}−\mathrm{10}−{b}\right){x}+{b}\left({a}−\mathrm{10}\right) \\ $$$$\:\:{c}\left({a}−\mathrm{10}\right)−\mathrm{1}\:=\:{b}\left({a}−\mathrm{6}\right)−\mathrm{1}\:\:\:\:\:…\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:{c}\left({a}−\mathrm{6}\right)={b}\left({a}−\mathrm{10}\right)\:\:\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\:\frac{{a}−\mathrm{10}}{{a}−\mathrm{6}}=\frac{{a}−\mathrm{6}}{{a}−\mathrm{10}} \\ $$$${or}\:\:\:\:\left({a}−\mathrm{10}\right)^{\mathrm{2}} =\:\left({a}−\mathrm{6}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\mathrm{20}{a}+\mathrm{100}\:=\:−\mathrm{12}{a}+\mathrm{36} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:\:{a}\:=\:\mathrm{8}\:\:. \\ $$
Commented by rahul 19 last updated on 01/Mar/18

$${thank}\:{u}\:{sir}! \\ $$
