Menu Close

Question-30961

Tinku Tara 0 Comments
Pin




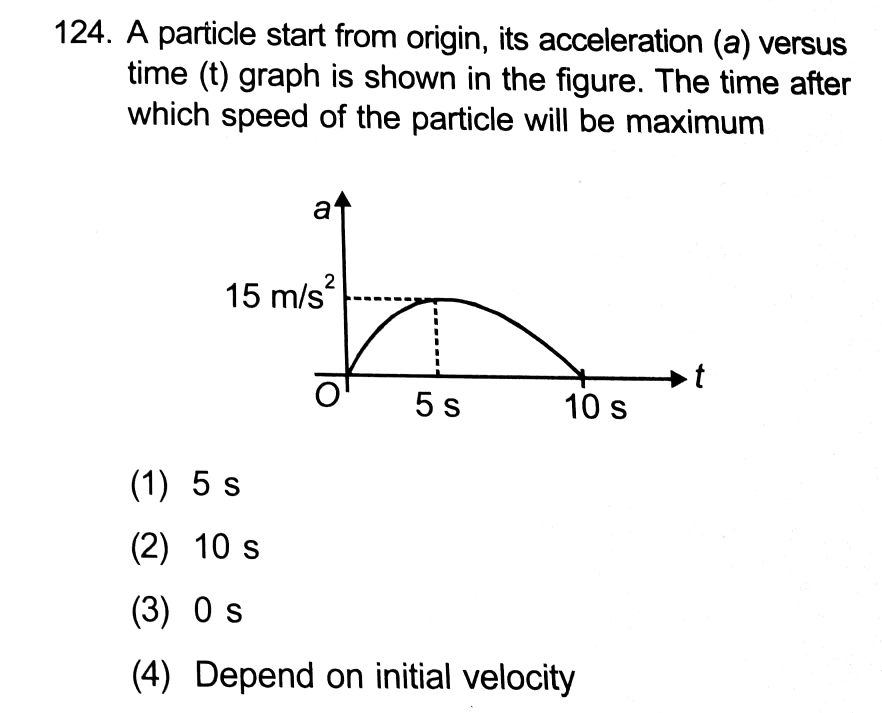
Question Number 30961 by Tinkutara last updated on 01/Mar/18
Commented by ajfour last updated on 01/Mar/18
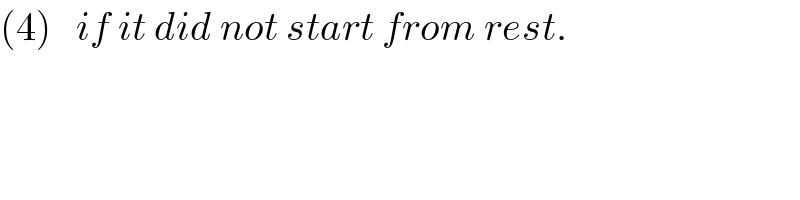
(4) if it did not start from rest.
$$\left(\mathrm{4}\right)\:\:\:{if}\:{it}\:{did}\:{not}\:{start}\:{from}\:{rest}. \\ $$
Commented by MJS last updated on 01/Mar/18
no. as long as the acc. is above zero, the speed will rise, no matter at which speed you start
$$\mathrm{no}.\:\mathrm{as}\:\mathrm{long}\:\mathrm{as}\:\mathrm{the}\:\mathrm{acc}.\:\mathrm{is}\:\mathrm{above}\: \\ $$$$\mathrm{zero},\:\mathrm{the}\:\mathrm{speed}\:\mathrm{will}\:\mathrm{rise},\:\mathrm{no}\:\mathrm{matter} \\ $$$$\mathrm{at}\:\mathrm{which}\:\mathrm{speed}\:\mathrm{you}\:\mathrm{start} \\ $$
Commented by ajfour last updated on 01/Mar/18
starts from origin OR starts from rest from origin, may be not the same.
$${starts}\:{from}\:{origin}\:{OR}\:\:{starts}\:{from} \\ $$$${rest}\:{from}\:{origin},\:{may}\:{be}\:{not}\:{the} \\ $$$${same}. \\ $$
Commented by Tinkutara last updated on 01/Mar/18
But how does it matter anyway? After 10 s it would be maximum because area under the curve will be maximum whether it starts from rest or not.
Commented by MJS last updated on 01/Mar/18
the graph shows the acceleration, not the velocity, so the answer is (2). you′re right
$$\mathrm{the}\:\mathrm{graph}\:\mathrm{shows}\:\mathrm{the}\:\mathrm{acceleration}, \\ $$$$\mathrm{not}\:\mathrm{the}\:\mathrm{velocity},\:\mathrm{so}\:\mathrm{the}\:\mathrm{answer} \\ $$$$\mathrm{is}\:\left(\mathrm{2}\right).\:\mathrm{you}'\mathrm{re}\:\mathrm{right} \\ $$
Commented by Tinkutara last updated on 01/Mar/18
No it is only 4⃣. Now got it. Thanks ajfour Sir.
Commented by MJS last updated on 01/Mar/18
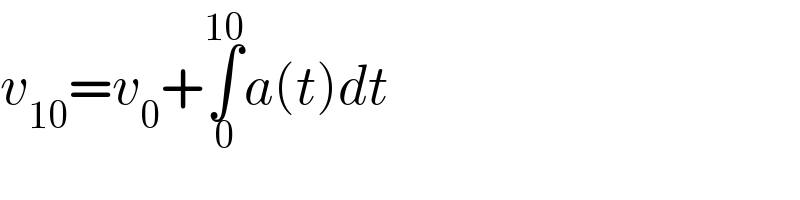
v_(10) =v_0 +∫_0 ^(10) a(t)dt
$${v}_{\mathrm{10}} ={v}_{\mathrm{0}} +\underset{\mathrm{0}} {\overset{\mathrm{10}} {\int}}{a}\left({t}\right){dt} \\ $$
Commented by ajfour last updated on 01/Mar/18
what if initial velocity is sufficiently negative , then due to positive acceleration, it will slow down..
$${what}\:{if}\:{initial}\:{velocity}\:{is} \\ $$$${sufficiently}\:{negative}\:,\:{then}\:{due} \\ $$$${to}\:{positive}\:{acceleration},\:{it}\:{will} \\ $$$${slow}\:{down}.. \\ $$
Commented by Tinkutara last updated on 01/Mar/18
Yes I also thought this way and it became clear.
Commented by MJS last updated on 01/Mar/18
velocity is always considered ≧0, if you drive 80 mph backwards, braking still slows you down. positive acceleration always speeds you up. if the given example would deal with n−dimensional vectors, it should be made clear somewhere. but then, the answer would also depend on the direction of acceleration. I would not put more into it than what′s obviously there...
$$\mathrm{velocity}\:\mathrm{is}\:\mathrm{always}\:\mathrm{considered}\:\geqq\mathrm{0},\:\mathrm{if} \\ $$$$\mathrm{you}\:\mathrm{drive}\:\mathrm{80}\:\mathrm{mph}\:\mathrm{backwards}, \\ $$$$\mathrm{braking}\:\mathrm{still}\:\mathrm{slows}\:\mathrm{you}\:\mathrm{down}. \\ $$$$\mathrm{positive}\:\mathrm{acceleration}\:\mathrm{always} \\ $$$$\mathrm{speeds}\:\mathrm{you}\:\mathrm{up}. \\ $$$$\mathrm{if}\:\mathrm{the}\:\mathrm{given}\:\mathrm{example}\:\mathrm{would}\:\mathrm{deal} \\ $$$$\mathrm{with}\:\mathrm{n}−\mathrm{dimensional}\:\mathrm{vectors},\: \\ $$$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{made}\:\mathrm{clear}\:\mathrm{somewhere}. \\ $$$$\mathrm{but}\:\mathrm{then},\:\mathrm{the}\:\mathrm{answer}\:\mathrm{would}\:\mathrm{also} \\ $$$$\mathrm{depend}\:\mathrm{on}\:\mathrm{the}\:\mathrm{direction}\:\mathrm{of} \\ $$$$\mathrm{acceleration}. \\ $$$$\mathrm{I}\:\mathrm{would}\:\mathrm{not}\:\mathrm{put}\:\mathrm{more}\:\mathrm{into}\:\mathrm{it} \\ $$$$\mathrm{than}\:\mathrm{what}'\mathrm{s}\:\mathrm{obviously}\:\mathrm{there}… \\ $$
Commented by MJS last updated on 01/Mar/18
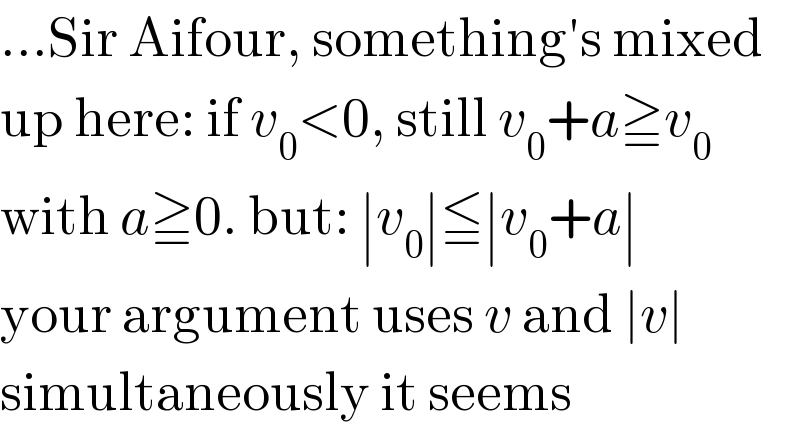
...Sir Aifour, something′s mixed up here: if v_0 <0, still v_0 +a≧v_0 with a≧0. but: ∣v_0 ∣≦∣v_0 +a∣ your argument uses v and ∣v∣ simultaneously it seems
$$…\mathrm{Sir}\:\mathrm{Aifour},\:\mathrm{something}'\mathrm{s}\:\mathrm{mixed} \\ $$$$\mathrm{up}\:\mathrm{here}:\:\mathrm{if}\:{v}_{\mathrm{0}} <\mathrm{0},\:\mathrm{still}\:{v}_{\mathrm{0}} +{a}\geqq{v}_{\mathrm{0}} \\ $$$$\mathrm{with}\:{a}\geqq\mathrm{0}.\:\mathrm{but}:\:\mid{v}_{\mathrm{0}} \mid\leqq\mid{v}_{\mathrm{0}} +{a}\mid \\ $$$$\mathrm{your}\:\mathrm{argument}\:\mathrm{uses}\:{v}\:\mathrm{and}\:\mid{v}\mid \\ $$$$\mathrm{simultaneously}\:\mathrm{it}\:\mathrm{seems} \\ $$
Commented by ajfour last updated on 01/Mar/18
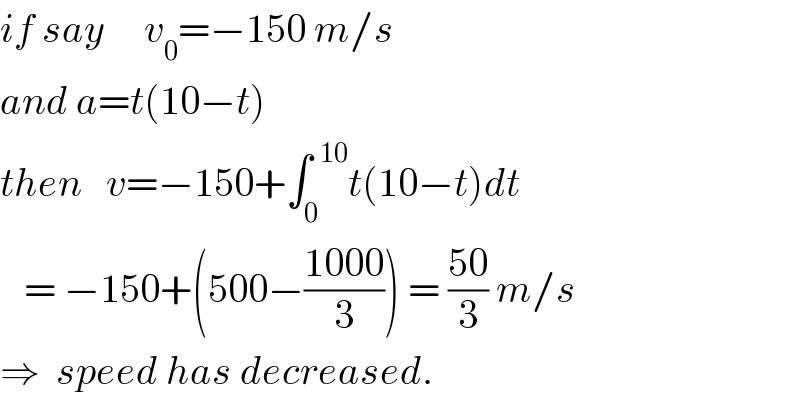
if say v_0 =−150 m/s and a=t(10−t) then v=−150+∫_0 ^( 10) t(10−t)dt = −150+(500−((1000)/3)) = ((50)/3) m/s ⇒ speed has decreased.
$${if}\:{say}\:\:\:\:\:{v}_{\mathrm{0}} =−\mathrm{150}\:{m}/{s} \\ $$$${and}\:{a}={t}\left(\mathrm{10}−{t}\right) \\ $$$${then}\:\:\:{v}=−\mathrm{150}+\int_{\mathrm{0}} ^{\:\:\mathrm{10}} {t}\left(\mathrm{10}−{t}\right){dt} \\ $$$$\:\:\:=\:−\mathrm{150}+\left(\mathrm{500}−\frac{\mathrm{1000}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{50}}{\mathrm{3}}\:{m}/{s} \\ $$$$\Rightarrow\:\:{speed}\:{has}\:{decreased}. \\ $$
Commented by MJS last updated on 01/Mar/18
I see what you mean but I believe the given problem isn′t meant this way. a moving particle accelerating gets faster. any other interpretation is possible but seems off topic.
$$\mathrm{I}\:\mathrm{see}\:\mathrm{what}\:\mathrm{you}\:\mathrm{mean} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{believe}\:\mathrm{the}\:\mathrm{given}\:\mathrm{problem} \\ $$$$\mathrm{isn}'\mathrm{t}\:\mathrm{meant}\:\mathrm{this}\:\mathrm{way}.\:\mathrm{a}\:\mathrm{moving} \\ $$$$\mathrm{particle}\:\mathrm{accelerating}\:\mathrm{gets}\:\mathrm{faster}. \\ $$$$\mathrm{any}\:\mathrm{other}\:\mathrm{interpretation}\:\mathrm{is}\: \\ $$$$\mathrm{possible}\:\mathrm{but}\:\mathrm{seems}\:\mathrm{off}\:\mathrm{topic}. \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *