Question-30990

Question Number 30990 by rahul 19 last updated on 01/Mar/18

Answered by MJS last updated on 01/Mar/18

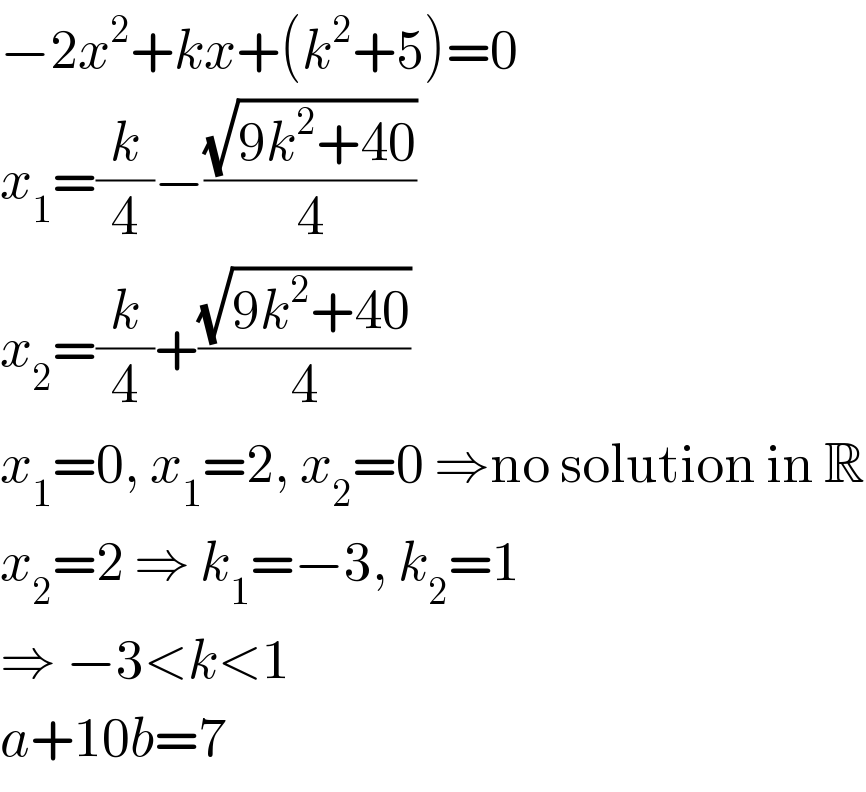
−2x^2 +kx+(k^2 +5)=0 x_1 =(k/4)−((√(9k^2 +40))/4) x_2 =(k/4)+((√(9k^2 +40))/4) x_1 =0, x_1 =2, x_2 =0 ⇒no solution in R x_2 =2 ⇒ k_1 =−3, k_2 =1 ⇒ −3<k<1 a+10b=7

$$−\mathrm{2}{x}^{\mathrm{2}} +{kx}+\left({k}^{\mathrm{2}} +\mathrm{5}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\frac{{k}}{\mathrm{4}}−\frac{\sqrt{\mathrm{9}{k}^{\mathrm{2}} +\mathrm{40}}}{\mathrm{4}} \\ $$$${x}_{\mathrm{2}} =\frac{{k}}{\mathrm{4}}+\frac{\sqrt{\mathrm{9}{k}^{\mathrm{2}} +\mathrm{40}}}{\mathrm{4}} \\ $$$${x}_{\mathrm{1}} =\mathrm{0},\:{x}_{\mathrm{1}} =\mathrm{2},\:{x}_{\mathrm{2}} =\mathrm{0}\:\Rightarrow\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathbb{R} \\ $$$${x}_{\mathrm{2}} =\mathrm{2}\:\Rightarrow\:{k}_{\mathrm{1}} =−\mathrm{3},\:{k}_{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\:−\mathrm{3}<{k}<\mathrm{1} \\ $$$${a}+\mathrm{10}{b}=\mathrm{7} \\ $$

Commented by rahul 19 last updated on 01/Mar/18

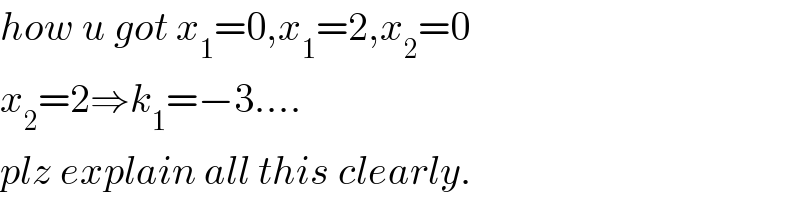
how u got x_1 =0,x_1 =2,x_2 =0 x_2 =2⇒k_1 =−3.... plz explain all this clearly.

$${how}\:{u}\:{got}\:{x}_{\mathrm{1}} =\mathrm{0},{x}_{\mathrm{1}} =\mathrm{2},{x}_{\mathrm{2}} =\mathrm{0} \\ $$$${x}_{\mathrm{2}} =\mathrm{2}\Rightarrow{k}_{\mathrm{1}} =−\mathrm{3}…. \\ $$$${plz}\:{explain}\:{all}\:{this}\:{clearly}. \\ $$

Commented by MJS last updated on 01/Mar/18

ok will do tomorrow morning, it′s 10:30 p.m. over here...

$$\mathrm{ok}\:\mathrm{will}\:\mathrm{do}\:\mathrm{tomorrow}\:\mathrm{morning},\:\mathrm{it}'\mathrm{s}\:\mathrm{10}:\mathrm{30}\:\mathrm{p}.\mathrm{m}. \\ $$$$\mathrm{over}\:\mathrm{here}… \\ $$

Commented by rahul 19 last updated on 03/Mar/18

$$?? \\ $$

Commented by MJS last updated on 04/Mar/18

sorry, I′m late... I set x on the borders, and solved the equations for x_1 , x_2 (these show that f(x) always has 2 distinct zeroes, because the root is ∈R^+ for k∈R) now I see it′s easier to set x=0 and x=2 in the original funktion and find the zeroes for k x=0 ⇒ k^2 +5=0 ⇒ no solution x=2 ⇒ k^2 +2k−3=0 ⇒ ⇒ k_1 =−3, k_2 =1 which means that one of the zeroes for x is on the border of the given interval when k is −3 or 1 the other zero is negative (easy to check with the x_1 −equation)

$$\mathrm{sorry},\:\mathrm{I}'\mathrm{m}\:\mathrm{late}… \\ $$$$\mathrm{I}\:\mathrm{set}\:{x}\:\mathrm{on}\:\mathrm{the}\:\mathrm{borders},\:\mathrm{and}\:\mathrm{solved} \\ $$$$\mathrm{the}\:\mathrm{equations}\:\mathrm{for}\:{x}_{\mathrm{1}} ,\:{x}_{\mathrm{2}} \\ $$$$\left(\mathrm{these}\:\mathrm{show}\:\mathrm{that}\:{f}\left({x}\right)\:\mathrm{always}\:\mathrm{has}\right. \\ $$$$\mathrm{2}\:\mathrm{distinct}\:\mathrm{zeroes},\:\mathrm{because}\:\mathrm{the}\:\mathrm{root}\: \\ $$$$\left.\mathrm{is}\:\in\mathbb{R}^{+} \:\mathrm{for}\:{k}\in\mathbb{R}\right) \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{I}\:\mathrm{see}\:\mathrm{it}'\mathrm{s}\:\mathrm{easier}\:\mathrm{to}\:\mathrm{set}\:{x}=\mathrm{0}\:\mathrm{and} \\ $$$${x}=\mathrm{2}\:\mathrm{in}\:\mathrm{the}\:\mathrm{original}\:\mathrm{funktion}\:\mathrm{and} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{zeroes}\:\mathrm{for}\:{k} \\ $$$${x}=\mathrm{0}\:\Rightarrow\:{k}^{\mathrm{2}} +\mathrm{5}=\mathrm{0}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$${x}=\mathrm{2}\:\Rightarrow\:{k}^{\mathrm{2}} +\mathrm{2}{k}−\mathrm{3}=\mathrm{0}\:\Rightarrow\: \\ $$$$\Rightarrow\:{k}_{\mathrm{1}} =−\mathrm{3},\:{k}_{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{which}\:\mathrm{means}\:\mathrm{that}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{zeroes} \\ $$$$\mathrm{for}\:{x}\:\mathrm{is}\:\mathrm{on}\:\mathrm{the}\:\mathrm{border}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{interval}\:\mathrm{when}\:{k}\:\mathrm{is}\:−\mathrm{3}\:\mathrm{or}\:\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{zero}\:\mathrm{is}\:\mathrm{negative}\:\left(\mathrm{easy}\:\mathrm{to}\right. \\ $$$$\left.\mathrm{check}\:\mathrm{with}\:\mathrm{the}\:{x}_{\mathrm{1}} −\mathrm{equation}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply