Question Number 31193 by Tinkutara last updated on 03/Mar/18

Answered by ajfour last updated on 03/Mar/18
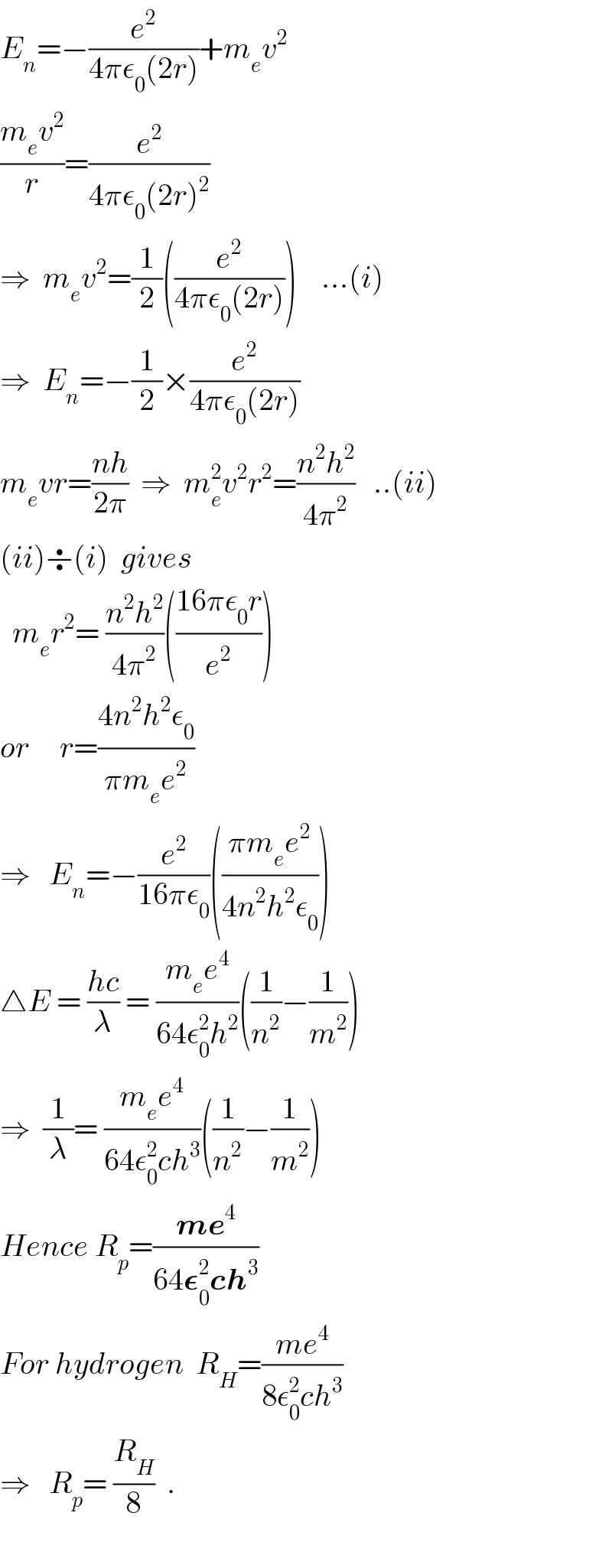
$${E}_{{n}} =−\frac{{e}^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left(\mathrm{2}{r}\right)}+{m}_{{e}} {v}^{\mathrm{2}} \\ $$$$\frac{{m}_{{e}} {v}^{\mathrm{2}} }{{r}}=\frac{{e}^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left(\mathrm{2}{r}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:{m}_{{e}} {v}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{e}^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left(\mathrm{2}{r}\right)}\right)\:\:\:\:…\left({i}\right) \\ $$$$\Rightarrow\:\:{E}_{{n}} =−\frac{\mathrm{1}}{\mathrm{2}}×\frac{{e}^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left(\mathrm{2}{r}\right)} \\ $$$${m}_{{e}} {vr}=\frac{{nh}}{\mathrm{2}\pi}\:\:\Rightarrow\:\:{m}_{{e}} ^{\mathrm{2}} {v}^{\mathrm{2}} {r}^{\mathrm{2}} =\frac{{n}^{\mathrm{2}} {h}^{\mathrm{2}} }{\mathrm{4}\pi^{\mathrm{2}} }\:\:\:..\left({ii}\right) \\ $$$$\left({ii}\right)\boldsymbol{\div}\left({i}\right)\:\:{gives} \\ $$$$\:\:{m}_{{e}} {r}^{\mathrm{2}} =\:\frac{{n}^{\mathrm{2}} {h}^{\mathrm{2}} }{\mathrm{4}\pi^{\mathrm{2}} }\left(\frac{\mathrm{16}\pi\epsilon_{\mathrm{0}} {r}}{{e}^{\mathrm{2}} }\right) \\ $$$${or}\:\:\:\:\:{r}=\frac{\mathrm{4}{n}^{\mathrm{2}} {h}^{\mathrm{2}} \epsilon_{\mathrm{0}} }{\pi{m}_{{e}} {e}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:{E}_{{n}} =−\frac{{e}^{\mathrm{2}} }{\mathrm{16}\pi\epsilon_{\mathrm{0}} }\left(\frac{\pi{m}_{{e}} {e}^{\mathrm{2}} }{\mathrm{4}{n}^{\mathrm{2}} {h}^{\mathrm{2}} \epsilon_{\mathrm{0}} }\right) \\ $$$$\bigtriangleup{E}\:=\:\frac{{hc}}{\lambda}\:=\:\frac{{m}_{{e}} {e}^{\mathrm{4}} }{\mathrm{64}\epsilon_{\mathrm{0}} ^{\mathrm{2}} {h}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{{m}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\lambda}=\:\frac{{m}_{{e}} {e}^{\mathrm{4}} }{\mathrm{64}\epsilon_{\mathrm{0}} ^{\mathrm{2}} {ch}^{\mathrm{3}} }\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{{m}^{\mathrm{2}} }\right) \\ $$$${Hence}\:{R}_{{p}} =\frac{\boldsymbol{{me}}^{\mathrm{4}} }{\mathrm{64}\boldsymbol{\epsilon}_{\mathrm{0}} ^{\mathrm{2}} \boldsymbol{{ch}}^{\mathrm{3}} } \\ $$$${For}\:{hydrogen}\:\:{R}_{{H}} =\frac{{me}^{\mathrm{4}} }{\mathrm{8}\epsilon_{\mathrm{0}} ^{\mathrm{2}} {ch}^{\mathrm{3}} } \\ $$$$\Rightarrow\:\:\:{R}_{{p}} =\:\frac{{R}_{{H}} }{\mathrm{8}}\:\:. \\ $$$$ \\ $$
