Question Number 31423 by mondodotto@gmail.com last updated on 08/Mar/18
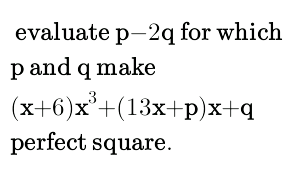
Commented by mondodotto@gmail.com last updated on 08/Mar/18

$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{help}}\:\boldsymbol{\mathrm{me}}! \\ $$
Answered by MJS last updated on 08/Mar/18
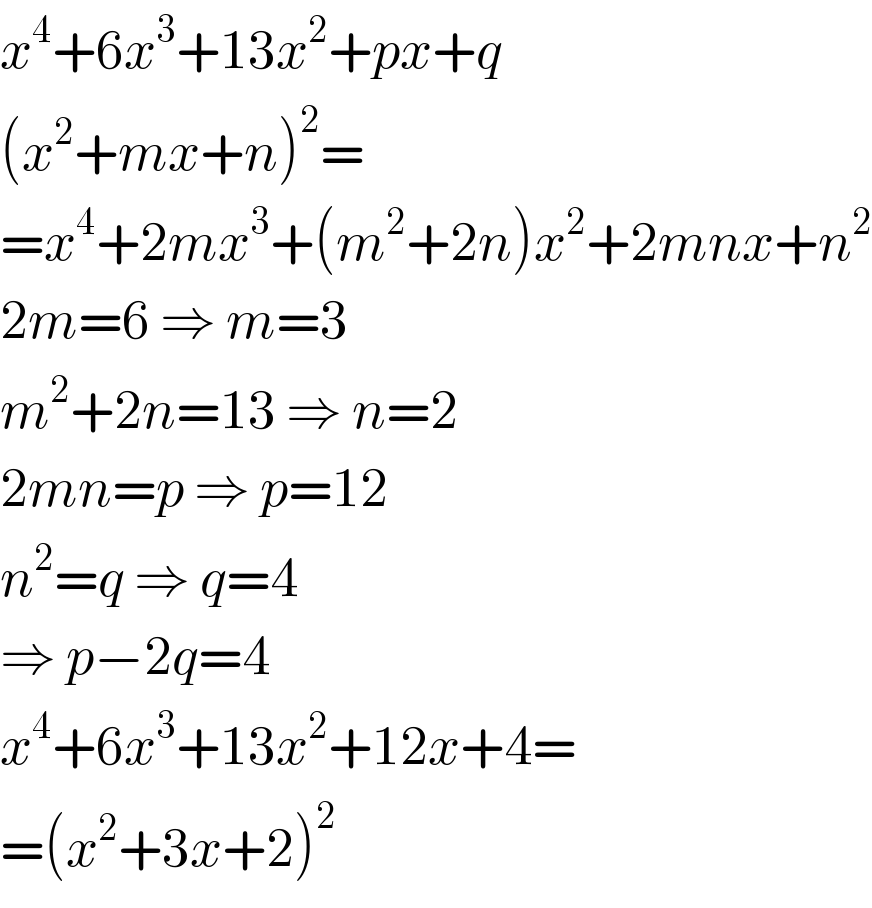
$${x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{3}} +\mathrm{13}{x}^{\mathrm{2}} +{px}+{q} \\ $$$$\left({x}^{\mathrm{2}} +{mx}+{n}\right)^{\mathrm{2}} = \\ $$$$={x}^{\mathrm{4}} +\mathrm{2}{mx}^{\mathrm{3}} +\left({m}^{\mathrm{2}} +\mathrm{2}{n}\right){x}^{\mathrm{2}} +\mathrm{2}{mnx}+{n}^{\mathrm{2}} \\ $$$$\mathrm{2}{m}=\mathrm{6}\:\Rightarrow\:{m}=\mathrm{3} \\ $$$${m}^{\mathrm{2}} +\mathrm{2}{n}=\mathrm{13}\:\Rightarrow\:{n}=\mathrm{2} \\ $$$$\mathrm{2}{mn}={p}\:\Rightarrow\:{p}=\mathrm{12} \\ $$$${n}^{\mathrm{2}} ={q}\:\Rightarrow\:{q}=\mathrm{4} \\ $$$$\Rightarrow\:{p}−\mathrm{2}{q}=\mathrm{4} \\ $$$${x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{3}} +\mathrm{13}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{4}= \\ $$$$=\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}\right)^{\mathrm{2}} \\ $$
Commented by mondodotto@gmail.com last updated on 08/Mar/18
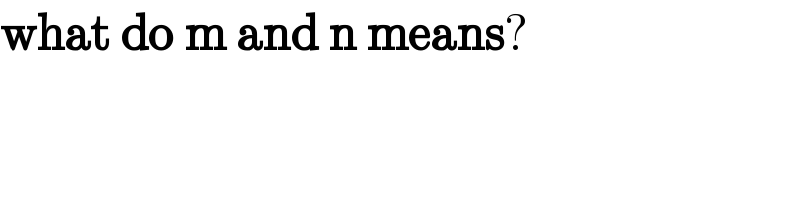
$$\boldsymbol{\mathrm{what}}\:\boldsymbol{\mathrm{do}}\:\boldsymbol{\mathrm{m}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{n}}\:\boldsymbol{\mathrm{means}}? \\ $$
Commented by rahul 19 last updated on 08/Mar/18

$${for}\:{the}\:{sake}\:{of}\:{solving}\:{they}\:{are}\:{just} \\ $$$${taken}\:{as}\:{the}\:{integral}\:{coefficients}\:. \\ $$
