Question Number 31436 by ajfour last updated on 08/Mar/18
Commented by ajfour last updated on 08/Mar/18

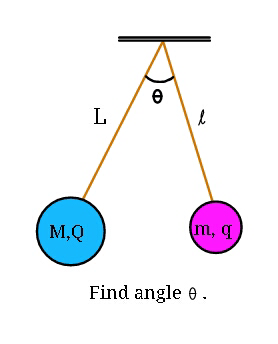
$${Two}\:{charged}\:{small}\:{balls}\:{are} \\ $$$${suspended}\:{by}\:{strings}\:{of}\:{length} \\ $$$${L}\:{and}\:{l}\:.\:{Find}\:{equilibrium}\:{angle}\:\theta\:. \\ $$
Commented by ajfour last updated on 08/Mar/18
Commented by ajfour last updated on 08/Mar/18
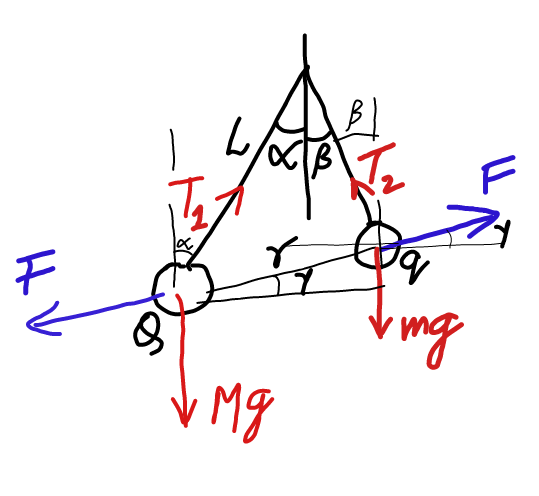
![Lsin α+lsin β=rcos γ Lcos α−lcos β=rsin γ From above two eqs. r, γ are determined. F=((Qq)/(4πε_0 r^2 )) T_1 cos α=Mg+Fsin γ T_1 sin α = Fcos γ ⇒ tan α = ((Fcos γ)/(Mg+Fsin γ)) similarly tan β = ((Fcos γ)/(mg−Fsin γ)) ⇒ θ=tan^(−1) [((((Fcos γ)/(Mg+Fsin γ))+((Fcos γ)/(mg−Fsin γ)))/(1−((F^( 2) cos^2 γ)/((Mg+Fsin γ)(mg−Fsin γ))))] .](https://www.tinkutara.com/question/Q31447.png)
$${L}\mathrm{sin}\:\alpha+{l}\mathrm{sin}\:\beta={r}\mathrm{cos}\:\gamma \\ $$$${L}\mathrm{cos}\:\alpha−{l}\mathrm{cos}\:\beta={r}\mathrm{sin}\:\gamma \\ $$$${From}\:{above}\:{two}\:{eqs}.\:{r},\:\gamma\:{are}\: \\ $$$${determined}. \\ $$$${F}=\frac{{Qq}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {r}^{\mathrm{2}} } \\ $$$${T}_{\mathrm{1}} \mathrm{cos}\:\alpha={Mg}+{F}\mathrm{sin}\:\gamma \\ $$$${T}_{\mathrm{1}} \mathrm{sin}\:\alpha\:=\:{F}\mathrm{cos}\:\gamma \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\alpha\:=\:\frac{{F}\mathrm{cos}\:\gamma}{{Mg}+{F}\mathrm{sin}\:\gamma} \\ $$$${similarly} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{tan}\:\beta\:=\:\frac{{F}\mathrm{cos}\:\gamma}{{mg}−{F}\mathrm{sin}\:\gamma} \\ $$$$\Rightarrow\:\theta=\mathrm{tan}^{−\mathrm{1}} \left[\frac{\frac{{F}\mathrm{cos}\:\gamma}{{Mg}+{F}\mathrm{sin}\:\gamma}+\frac{{F}\mathrm{cos}\:\gamma}{{mg}−{F}\mathrm{sin}\:\gamma}}{\mathrm{1}−\frac{{F}^{\:\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \gamma}{\left({Mg}+{F}\mathrm{sin}\:\gamma\right)\left({mg}−{F}\mathrm{sin}\:\gamma\right.}}\right]\:. \\ $$
