Question Number 31441 by mondodotto@gmail.com last updated on 08/Mar/18
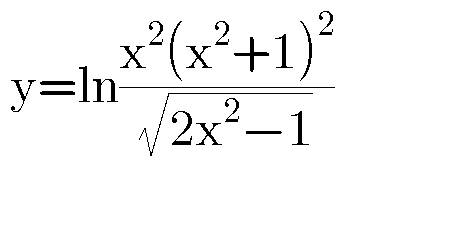
Commented by mondodotto@gmail.com last updated on 08/Mar/18

$$\boldsymbol{\mathrm{differentiate}} \\ $$
Answered by MJS last updated on 08/Mar/18
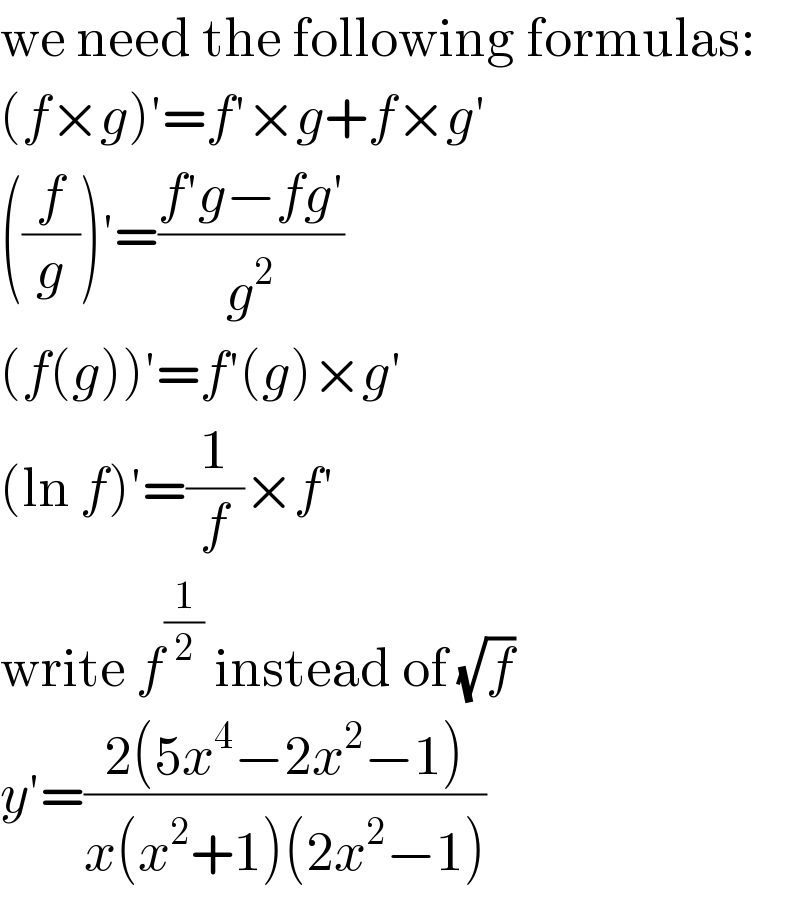
$$\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{following}\:\mathrm{formulas}: \\ $$$$\left({f}×{g}\right)'={f}'×{g}+{f}×{g}' \\ $$$$\left(\frac{{f}}{{g}}\right)'=\frac{{f}'{g}−{fg}'}{{g}^{\mathrm{2}} } \\ $$$$\left({f}\left({g}\right)\right)'={f}'\left({g}\right)×{g}' \\ $$$$\left(\mathrm{ln}\:{f}\right)'=\frac{\mathrm{1}}{{f}}×{f}' \\ $$$$\mathrm{write}\:{f}^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{instead}\:\mathrm{of}\:\sqrt{{f}} \\ $$$${y}'=\frac{\mathrm{2}\left(\mathrm{5}{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$
