Menu Close

Question-31485

Tinku Tara 0 Comments
Pin




Question Number 31485 by mondodotto@gmail.com last updated on 09/Mar/18
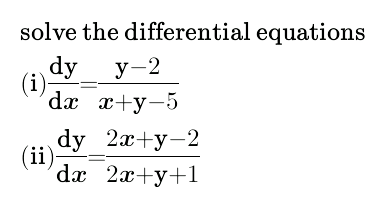
Answered by ajfour last updated on 09/Mar/18
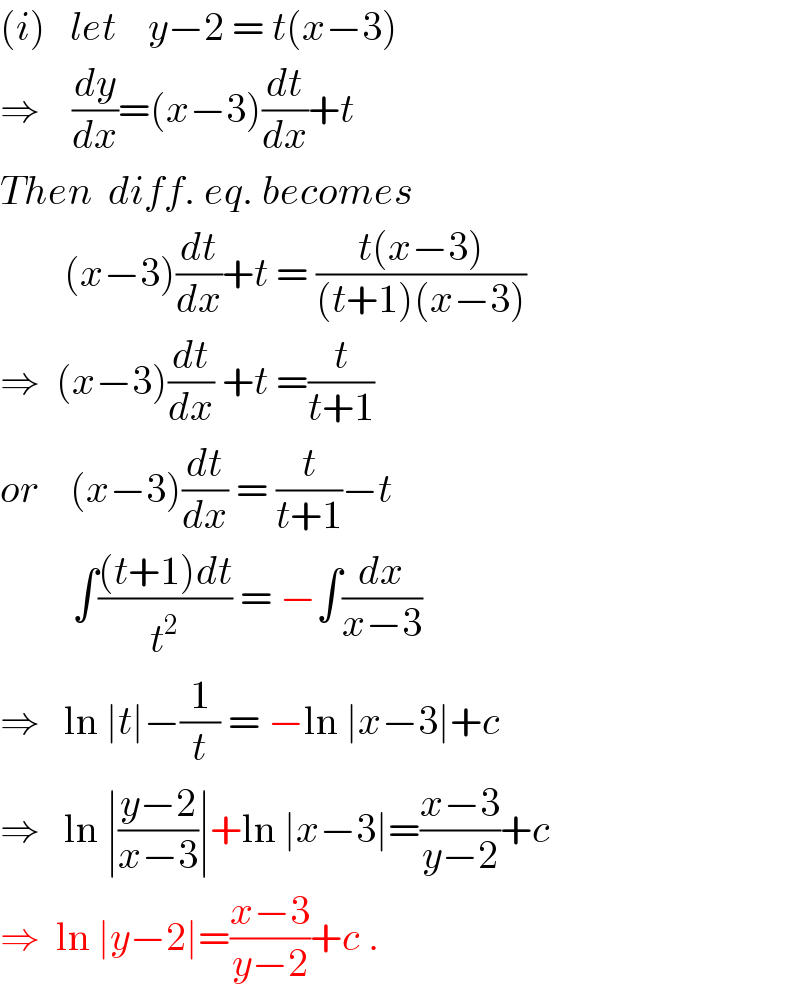
(i) let y−2 = t(x−3) ⇒ (dy/dx)=(x−3)(dt/dx)+t Then diff. eq. becomes (x−3)(dt/dx)+t = ((t(x−3))/((t+1)(x−3))) ⇒ (x−3)(dt/dx) +t =(t/(t+1)) or (x−3)(dt/dx) = (t/(t+1))−t ∫(((t+1)dt)/t^2 ) = −∫(dx/(x−3)) ⇒ ln ∣t∣−(1/t) = −ln ∣x−3∣+c ⇒ ln ∣((y−2)/(x−3))∣+ln ∣x−3∣=((x−3)/(y−2))+c ⇒ ln ∣y−2∣=((x−3)/(y−2))+c .
$$\left({i}\right)\:\:\:{let}\:\:\:\:{y}−\mathrm{2}\:=\:{t}\left({x}−\mathrm{3}\right) \\ $$$$\Rightarrow\:\:\:\:\frac{{dy}}{{dx}}=\left({x}−\mathrm{3}\right)\frac{{dt}}{{dx}}+{t} \\ $$$${Then}\:\:{diff}.\:{eq}.\:{becomes} \\ $$$$\:\:\:\:\:\:\:\:\left({x}−\mathrm{3}\right)\frac{{dt}}{{dx}}+{t}\:=\:\frac{{t}\left({x}−\mathrm{3}\right)}{\left({t}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)} \\ $$$$\Rightarrow\:\:\left({x}−\mathrm{3}\right)\frac{{dt}}{{dx}}\:+{t}\:=\frac{{t}}{{t}+\mathrm{1}} \\ $$$${or}\:\:\:\:\left({x}−\mathrm{3}\right)\frac{{dt}}{{dx}}\:=\:\frac{{t}}{{t}+\mathrm{1}}−{t} \\ $$$$\:\:\:\:\:\:\:\:\:\int\frac{\left({t}+\mathrm{1}\right){dt}}{{t}^{\mathrm{2}} }\:=\:−\int\frac{{dx}}{{x}−\mathrm{3}} \\ $$$$\Rightarrow\:\:\:\mathrm{ln}\:\mid{t}\mid−\frac{\mathrm{1}}{{t}}\:=\:−\mathrm{ln}\:\mid{x}−\mathrm{3}\mid+{c} \\ $$$$\Rightarrow\:\:\:\mathrm{ln}\:\mid\frac{{y}−\mathrm{2}}{{x}−\mathrm{3}}\mid+\mathrm{ln}\:\mid{x}−\mathrm{3}\mid=\frac{{x}−\mathrm{3}}{{y}−\mathrm{2}}+{c}\: \\ $$$$\Rightarrow\:\:\mathrm{ln}\:\mid{y}−\mathrm{2}\mid=\frac{{x}−\mathrm{3}}{{y}−\mathrm{2}}+{c}\:. \\ $$
Answered by ajfour last updated on 09/Mar/18
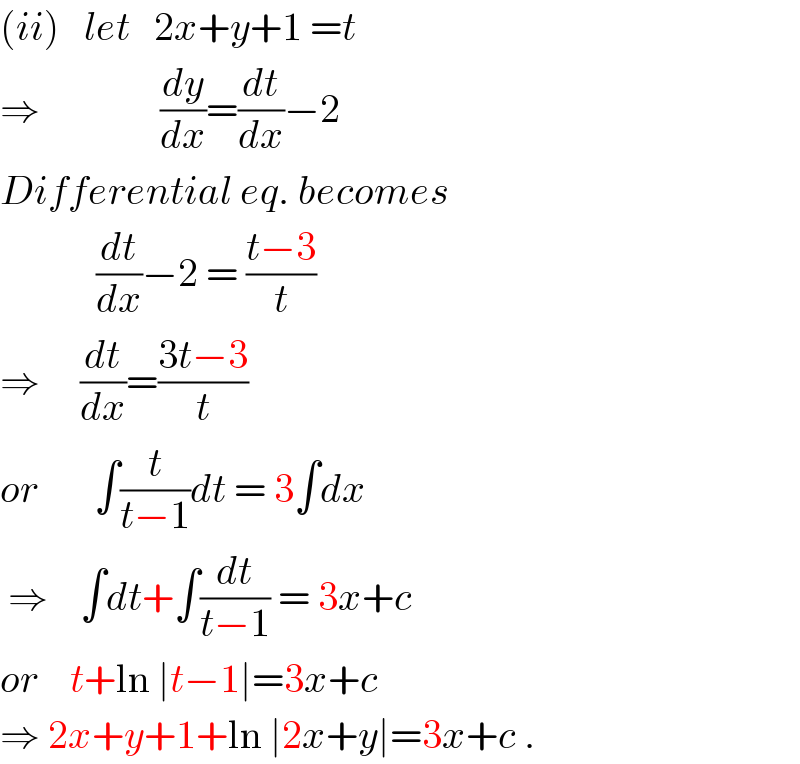
(ii) let 2x+y+1 =t ⇒ (dy/dx)=(dt/dx)−2 Differential eq. becomes (dt/dx)−2 = ((t−3)/t) ⇒ (dt/dx)=((3t−3)/t) or ∫(t/(t−1))dt = 3∫dx ⇒ ∫dt+∫(dt/(t−1)) = 3x+c or t+ln ∣t−1∣=3x+c ⇒ 2x+y+1+ln ∣2x+y∣=3x+c .
$$\left({ii}\right)\:\:\:{let}\:\:\:\mathrm{2}{x}+{y}+\mathrm{1}\:={t} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{dy}}{{dx}}=\frac{{dt}}{{dx}}−\mathrm{2} \\ $$$${Differential}\:{eq}.\:{becomes} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{{dt}}{{dx}}−\mathrm{2}\:=\:\frac{{t}−\mathrm{3}}{{t}} \\ $$$$\Rightarrow\:\:\:\:\:\frac{{dt}}{{dx}}=\frac{\mathrm{3}{t}−\mathrm{3}}{{t}} \\ $$$${or}\:\:\:\:\:\:\:\int\frac{{t}}{{t}−\mathrm{1}}{dt}\:=\:\mathrm{3}\int{dx} \\ $$$$\:\Rightarrow\:\:\:\:\int{dt}+\int\frac{{dt}}{{t}−\mathrm{1}}\:=\:\mathrm{3}{x}+{c} \\ $$$${or}\:\:\:\:{t}+\mathrm{ln}\:\mid{t}−\mathrm{1}\mid=\mathrm{3}{x}+{c} \\ $$$$\Rightarrow\:\mathrm{2}{x}+{y}+\mathrm{1}+\mathrm{ln}\:\mid\mathrm{2}{x}+{y}\mid=\mathrm{3}{x}+{c}\:. \\ $$
Commented by mondodotto@gmail.com last updated on 09/Mar/18
thanx a lot.
$$\mathrm{thanx}\:\mathrm{a}\:\mathrm{lot}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *