Question Number 31571 by mondodotto@gmail.com last updated on 10/Mar/18
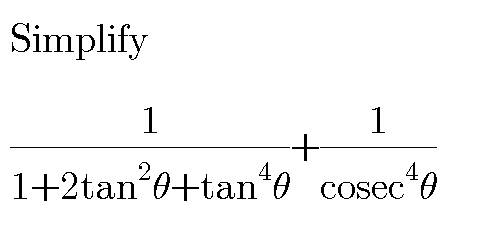
Answered by Joel578 last updated on 10/Mar/18
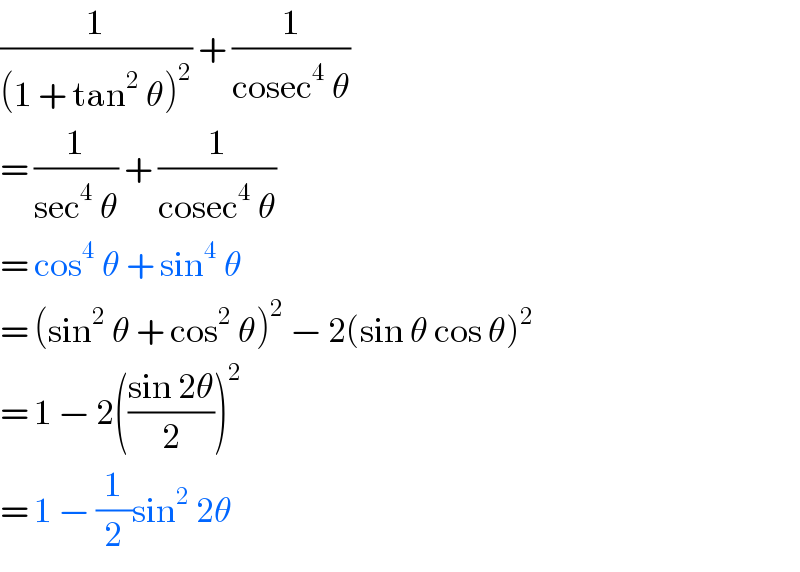
$$\frac{\mathrm{1}}{\left(\mathrm{1}\:+\:\mathrm{tan}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{cosec}^{\mathrm{4}} \:\theta} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{sec}^{\mathrm{4}} \:\theta}\:+\:\frac{\mathrm{1}}{\mathrm{cosec}^{\mathrm{4}} \:\theta} \\ $$$$=\:\mathrm{cos}^{\mathrm{4}} \:\theta\:+\:\mathrm{sin}^{\mathrm{4}} \:\theta \\ $$$$=\:\left(\mathrm{sin}^{\mathrm{2}} \:\theta\:+\:\mathrm{cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{2}} \:−\:\mathrm{2}\left(\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$$=\:\mathrm{1}\:−\:\mathrm{2}\left(\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=\:\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\theta \\ $$
Answered by rahul 19 last updated on 10/Mar/18
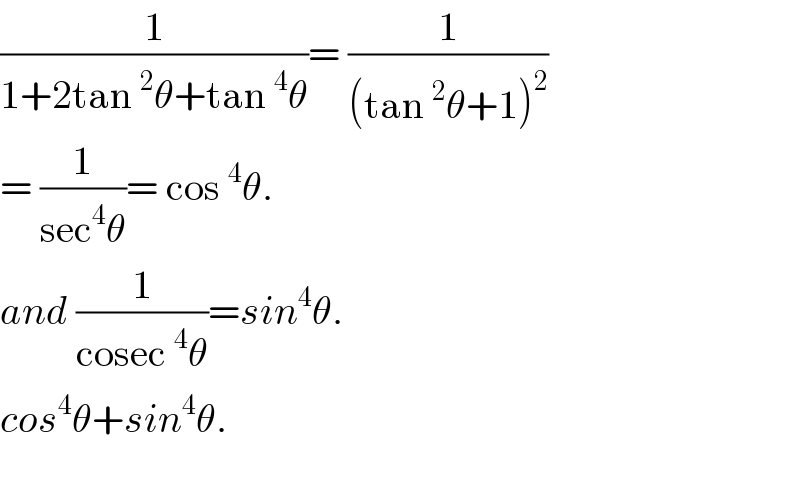
$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2tan}\:^{\mathrm{2}} \theta+\mathrm{tan}\:^{\mathrm{4}} \theta}=\:\frac{\mathrm{1}}{\left(\mathrm{tan}\:^{\mathrm{2}} \theta+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{sec}^{\mathrm{4}} \theta}=\:\mathrm{cos}\:^{\mathrm{4}} \theta. \\ $$$${and}\:\frac{\mathrm{1}}{\mathrm{cosec}\:^{\mathrm{4}} \theta}={sin}^{\mathrm{4}} \theta. \\ $$$${cos}^{\mathrm{4}} \theta+{sin}^{\mathrm{4}} \theta. \\ $$$$ \\ $$
