Question Number 31594 by Nayon.Sm last updated on 11/Mar/18
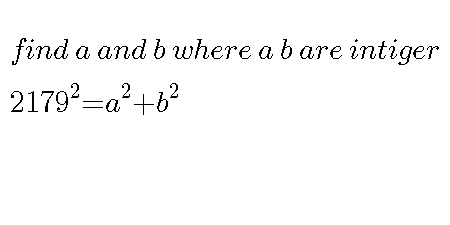
Answered by Rasheed.Sindhi last updated on 11/Mar/18

$${a}=\mathrm{0}\:\mid\:{b}=\mathrm{0}\:;\:\mathrm{No}\:\mathrm{other}\:\mathrm{integral}\:\mathrm{solution}. \\ $$$$−.−.−.−.−.−.− \\ $$$$\mathrm{If}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} \:\mathrm{then}\:\mathrm{there}\:\mathrm{exist}\:\mathrm{integers} \\ $$$${m}\:\&\:{n}\:\mathrm{such}\:\mathrm{that}\:{c}={m}^{\mathrm{2}} +{n}^{\mathrm{2}} \:,\left\{{a},{b}\right\}=\left\{{m}^{\mathrm{2}} -{n}^{\mathrm{2}} ,\mathrm{2}{mn}\right\} \\ $$$$\mathrm{So}\:\mathrm{we}\:\mathrm{have}\:{m}^{\mathrm{2}} +{n}^{\mathrm{2}} ={c}=\mathrm{2179} \\ $$$$\:\:\:\:\:\:\:\:\:\:{n}^{\mathrm{2}} =\mathrm{2179}−{m}^{\mathrm{2}} \\ $$$$\:\mathrm{I}-\mathrm{e}\:\:\mathrm{2179}−{m}^{\mathrm{2}} \:\:\mathrm{is}\:\mathrm{perfect}\:\mathrm{square}\:\mathrm{of}\:\mathrm{an} \\ $$$$\mathrm{integer}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{m}^{\mathrm{2}} \leqslant\mathrm{2179}\Rightarrow{m}\leqslant\mathrm{46} \\ $$$${m}\in\left\{\mathrm{0},\pm\mathrm{1},\pm\mathrm{2},\pm\mathrm{3},…,\pm\mathrm{46}\right\} \\ $$$$\mathrm{For}\:\mathrm{no}\:\mathrm{value}\:\mathrm{of}\:{m}\:\:\mathrm{2179}−{m}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{perfect} \\ $$$$\mathrm{square}. \\ $$$$ \\ $$
