Question Number 31734 by mondodotto@gmail.com last updated on 13/Mar/18
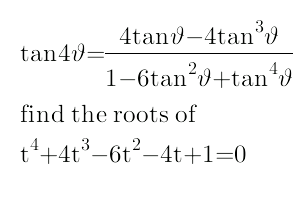
Answered by Tinkutara last updated on 13/Mar/18
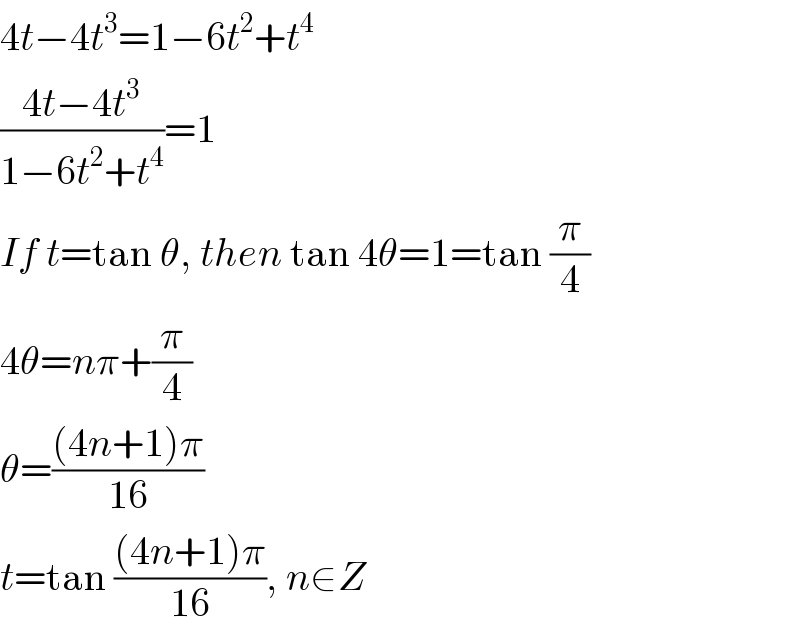
$$\mathrm{4}{t}−\mathrm{4}{t}^{\mathrm{3}} =\mathrm{1}−\mathrm{6}{t}^{\mathrm{2}} +{t}^{\mathrm{4}} \\ $$$$\frac{\mathrm{4}{t}−\mathrm{4}{t}^{\mathrm{3}} }{\mathrm{1}−\mathrm{6}{t}^{\mathrm{2}} +{t}^{\mathrm{4}} }=\mathrm{1} \\ $$$${If}\:{t}=\mathrm{tan}\:\theta,\:{then}\:\mathrm{tan}\:\mathrm{4}\theta=\mathrm{1}=\mathrm{tan}\:\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{4}\theta={n}\pi+\frac{\pi}{\mathrm{4}} \\ $$$$\theta=\frac{\left(\mathrm{4}{n}+\mathrm{1}\right)\pi}{\mathrm{16}} \\ $$$${t}=\mathrm{tan}\:\frac{\left(\mathrm{4}{n}+\mathrm{1}\right)\pi}{\mathrm{16}},\:{n}\in{Z} \\ $$
Commented by mondodotto@gmail.com last updated on 13/Mar/18
$$\mathrm{please}\:\mathrm{recheck} \\ $$
Commented by Tinkutara last updated on 13/Mar/18
Yes it is correct
