Question Number 31822 by Tinkutara last updated on 15/Mar/18
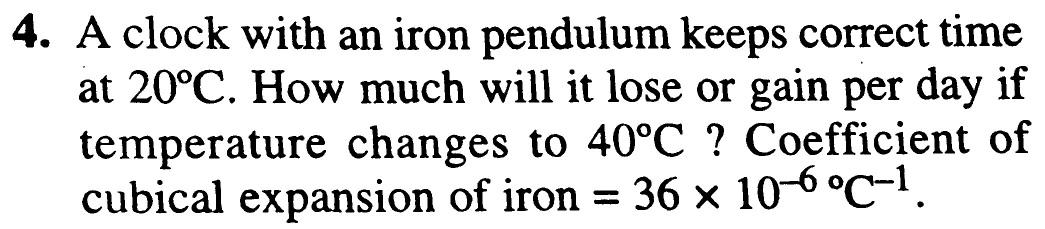
Answered by rahul 19 last updated on 15/Mar/18

$$\mathrm{10}.\mathrm{368}\:{sec}\:\left({loose}\right)\:. \\ $$$${the}\:{formula}\:{is}\:\Delta{T}=\:\frac{\mathrm{1}}{\mathrm{2}}\alpha\left(\Delta\theta\right){T} \\ $$$${here}\:\gamma\:=\:\mathrm{36}×\mathrm{10}^{−\mathrm{6}} \:{and} \\ $$$${we}\:{know}\:\mathrm{3}\alpha=\gamma\: \\ $$$$\Rightarrow\:\alpha\:=\:\mathrm{12}×\mathrm{10}^{−\mathrm{6}} . \\ $$$${plugging}\:{the}\:{values}\:{in}\:{formula}\:{we}\:{get}, \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}.\:\mathrm{12}×\mathrm{10}^{−\mathrm{6}} .\:\left(\mathrm{40}−\mathrm{20}\right).\mathrm{24}.\mathrm{60}.\mathrm{60} \\ $$$$\Rightarrow\:\mathrm{10}.\mathrm{368}\:{sec}. \\ $$
Commented by Tinkutara last updated on 15/Mar/18
Correct, can you please explain? Actually I know the method but initial time period should be taken 1s or 2s?
Commented by rahul 19 last updated on 15/Mar/18
$${i}\:{am}\:{not}\:{able}\:{to}\:{understand}\:\:,\:{what}\: \\ $$$${are}\:{u}\:{trying}\:{to}\:{say}? \\ $$
Commented by Tinkutara last updated on 15/Mar/18
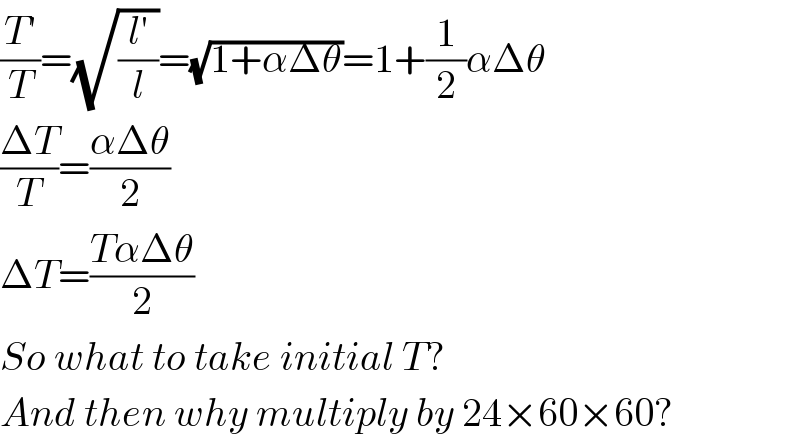
$$\frac{{T}'}{{T}}=\sqrt{\frac{{l}'}{{l}}}=\sqrt{\mathrm{1}+\alpha\Delta\theta}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\alpha\Delta\theta \\ $$$$\frac{\Delta{T}}{{T}}=\frac{\alpha\Delta\theta}{\mathrm{2}} \\ $$$$\Delta{T}=\frac{{T}\alpha\Delta\theta}{\mathrm{2}} \\ $$$${So}\:{what}\:{to}\:{take}\:{initial}\:{T}? \\ $$$${And}\:{then}\:{why}\:{multiply}\:{by}\:\mathrm{24}×\mathrm{60}×\mathrm{60}? \\ $$
Commented by rahul 19 last updated on 15/Mar/18
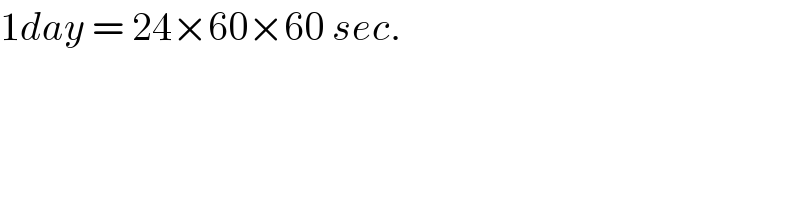
$$\mathrm{1}{day}\:=\:\mathrm{24}×\mathrm{60}×\mathrm{60}\:{sec}. \\ $$
Commented by Tinkutara last updated on 15/Mar/18
Did you take here T=1s?
Commented by rahul 19 last updated on 15/Mar/18
$${no}\:{i}\:{have}\:{taken}\:\mathrm{1}\:{day}\:{as}\:{mentioned}\: \\ $$$${in}\:{q}\:.\:\left(\:{loose}\:/\:{gain}\:{per}\:{day}\right). \\ $$
Commented by Tinkutara last updated on 15/Mar/18
Thank you very much Sir! I got the answer. ��������
