Question-32098

Facebook Tweet Pin

Question Number 32098 by Tinkutara last updated on 19/Mar/18

Commented by ajfour last updated on 19/Mar/18

$$\frac{\mathrm{3}{L}}{\mathrm{4}}\:\:. \\ $$

Commented by Tinkutara last updated on 19/Mar/18

Yes correct. Did you use torque balancing or COM concept?

Commented by ajfour last updated on 19/Mar/18

$${com}\:{concept}. \\ $$

Commented by mrW2 last updated on 19/Mar/18

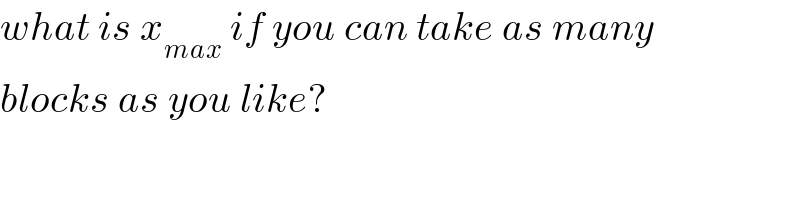
$${what}\:{is}\:{x}_{{max}} \:{if}\:{you}\:{can}\:{take}\:{as}\:{many} \\ $$$${blocks}\:{as}\:{you}\:{like}? \\ $$

Commented by mrW2 last updated on 20/Mar/18

Commented by mrW2 last updated on 20/Mar/18

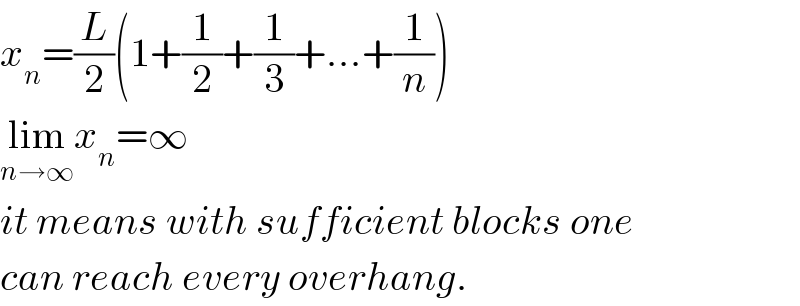
x_n =(L/2)(1+(1/2)+(1/3)+...+(1/n)) lim_(n→∞) x_n =∞ it means with sufficient blocks one can reach every overhang.

$${x}_{{n}} =\frac{{L}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{{n}}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{x}_{{n}} =\infty \\ $$$${it}\:{means}\:{with}\:{sufficient}\:{blocks}\:{one} \\ $$$${can}\:{reach}\:{every}\:{overhang}. \\ $$

Commented by Tinkutara last updated on 20/Mar/18

@ajfour Sir please show COM concept. I can't solve by that method.

Commented by Tinkutara last updated on 20/Mar/18

$$@{mrW}\mathrm{2}\:{Sir}\:{how} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{x}_{{n}} =\infty \\ $$$$? \\ $$

Commented by mrW2 last updated on 20/Mar/18

the harminic series is divergent. x_(n+1) >x_n ⇒lim_(n→∞) x_n =∞ proof: assume it converges, i.e. S=1+(1/2)+(1/3)+(1/4)+(1/5)+(1/6).... S>1+(1/2)+(1/4)+(1/4)+(1/6)+(1/6).... =(1/2)+(1/2)+(1/2)+(1/4)+(1/4)+(1/6)+(1/6).... =(1/2)+(1+(1/2)+(1/3)+(1/4)+....) ⇒S>(1/2)+S this is contradiction.

$${the}\:{harminic}\:{series}\:{is}\:{divergent}. \\ $$$${x}_{{n}+\mathrm{1}} >{x}_{{n}} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}{x}_{{n}} =\infty \\ $$$$ \\ $$$${proof}: \\ $$$${assume}\:{it}\:{converges},\:{i}.{e}. \\ $$$${S}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{6}}…. \\ $$$${S}>\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{6}}…. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{6}}…. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+….\right) \\ $$$$\Rightarrow{S}>\frac{\mathrm{1}}{\mathrm{2}}+{S} \\ $$$${this}\:{is}\:{contradiction}. \\ $$

Commented by Tinkutara last updated on 20/Mar/18

Thank you very much Sir! ��

Commented by abdo imad last updated on 20/Mar/18

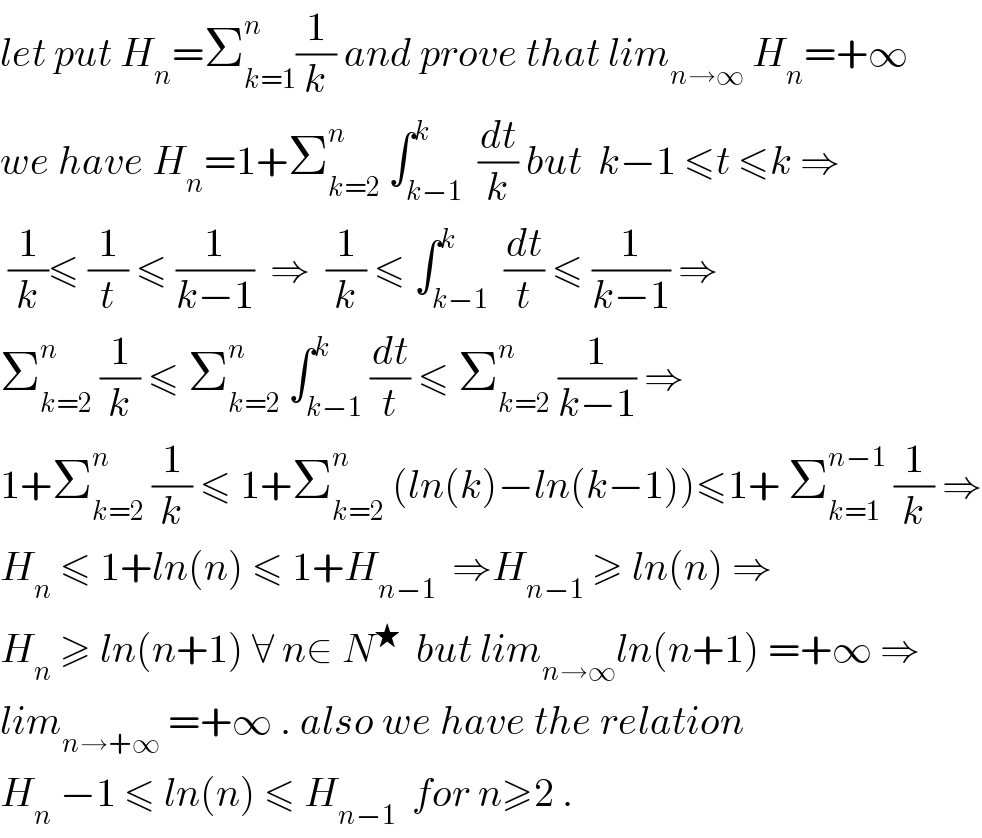
let put H_n =Σ_(k=1) ^n (1/k) and prove that lim_(n→∞) H_n =+∞ we have H_n =1+Σ_(k=2) ^n ∫_(k−1) ^k (dt/k) but k−1 ≤t ≤k ⇒ (1/k)≤ (1/t) ≤ (1/(k−1)) ⇒ (1/k) ≤ ∫_(k−1) ^k (dt/t) ≤ (1/(k−1)) ⇒ Σ_(k=2) ^n (1/k) ≤ Σ_(k=2) ^n ∫_(k−1) ^k (dt/t) ≤ Σ_(k=2) ^n (1/(k−1)) ⇒ 1+Σ_(k=2) ^n (1/k) ≤ 1+Σ_(k=2) ^n (ln(k)−ln(k−1))≤1+ Σ_(k=1) ^(n−1) (1/k) ⇒ H_n ≤ 1+ln(n) ≤ 1+H_(n−1) ⇒H_(n−1) ≥ ln(n) ⇒ H_n ≥ ln(n+1) ∀ n∈ N^★ but lim_(n→∞) ln(n+1) =+∞ ⇒ lim_(n→+∞) =+∞ . also we have the relation H_n −1 ≤ ln(n) ≤ H_(n−1) for n≥2 .

$${let}\:{put}\:{H}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{{k}}\:{and}\:{prove}\:{that}\:{lim}_{{n}\rightarrow\infty} \:{H}_{{n}} =+\infty \\ $$$${we}\:{have}\:{H}_{{n}} =\mathrm{1}+\sum_{{k}=\mathrm{2}} ^{{n}} \:\int_{{k}−\mathrm{1}} ^{{k}} \:\frac{{dt}}{{k}}\:{but}\:\:{k}−\mathrm{1}\:\leqslant{t}\:\leqslant{k}\:\Rightarrow \\ $$$$\:\frac{\mathrm{1}}{{k}}\leqslant\:\frac{\mathrm{1}}{{t}}\:\leqslant\:\frac{\mathrm{1}}{{k}−\mathrm{1}}\:\:\Rightarrow\:\:\frac{\mathrm{1}}{{k}}\:\leqslant\:\int_{{k}−\mathrm{1}} ^{{k}} \:\frac{{dt}}{{t}}\:\leqslant\:\frac{\mathrm{1}}{{k}−\mathrm{1}}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:\leqslant\:\sum_{{k}=\mathrm{2}} ^{{n}} \:\int_{{k}−\mathrm{1}} ^{{k}} \frac{{dt}}{{t}}\:\leqslant\:\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}−\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{1}+\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:\leqslant\:\mathrm{1}+\sum_{{k}=\mathrm{2}} ^{{n}} \:\left({ln}\left({k}\right)−{ln}\left({k}−\mathrm{1}\right)\right)\leqslant\mathrm{1}+\:\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}}\:\Rightarrow \\ $$$${H}_{{n}} \:\leqslant\:\mathrm{1}+{ln}\left({n}\right)\:\leqslant\:\mathrm{1}+{H}_{{n}−\mathrm{1}} \:\:\Rightarrow{H}_{{n}−\mathrm{1}} \:\geqslant\:{ln}\left({n}\right)\:\Rightarrow \\ $$$${H}_{{n}} \:\geqslant\:{ln}\left({n}+\mathrm{1}\right)\:\forall\:{n}\in\:{N}^{\bigstar} \:\:{but}\:{lim}_{{n}\rightarrow\infty} {ln}\left({n}+\mathrm{1}\right)\:=+\infty\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:=+\infty\:.\:{also}\:{we}\:{have}\:{the}\:{relation} \\ $$$${H}_{{n}} \:−\mathrm{1}\:\leqslant\:{ln}\left({n}\right)\:\leqslant\:{H}_{{n}−\mathrm{1}} \:\:{for}\:{n}\geqslant\mathrm{2}\:. \\ $$

Commented by Tinkutara last updated on 21/Mar/18

Thank you abdo imad Sir!

Commented by abdo imad last updated on 21/Mar/18

$${nevermind}\:{sir} \\ $$

Commented by mrW2 last updated on 22/Mar/18

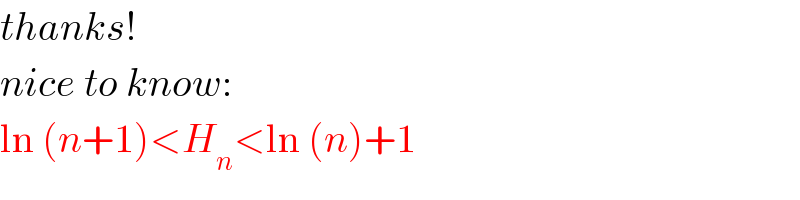
thanks! nice to know: ln (n+1)<H_n <ln (n)+1

$${thanks}! \\ $$$${nice}\:{to}\:{know}: \\ $$$$\mathrm{ln}\:\left({n}+\mathrm{1}\right)<{H}_{{n}} <\mathrm{ln}\:\left({n}\right)+\mathrm{1} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply