Question Number 32126 by mondodotto@gmail.com last updated on 20/Mar/18
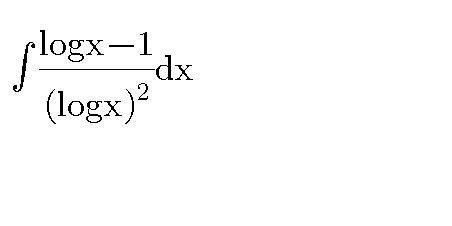
Commented by mondodotto@gmail.com last updated on 20/Mar/18

$$\boldsymbol{{please}}\:\boldsymbol{{help}} \\ $$
Answered by mrW2 last updated on 20/Mar/18
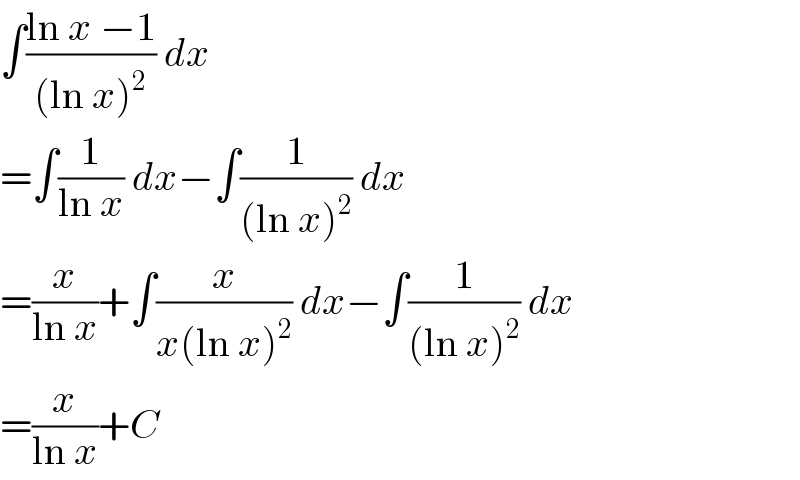
$$\int\frac{\mathrm{ln}\:{x}\:−\mathrm{1}}{\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} }\:{dx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{ln}\:{x}}\:{dx}−\int\frac{\mathrm{1}}{\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} }\:{dx} \\ $$$$=\frac{{x}}{\mathrm{ln}\:{x}}+\int\frac{{x}}{{x}\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} }\:{dx}−\int\frac{\mathrm{1}}{\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} }\:{dx} \\ $$$$=\frac{{x}}{\mathrm{ln}\:{x}}+{C} \\ $$
Commented by mondodotto@gmail.com last updated on 20/Mar/18

$$\mathrm{thanx}\:\mathrm{a}\:\mathrm{lot} \\ $$
