Question Number 32211 by mondodotto@gmail.com last updated on 21/Mar/18
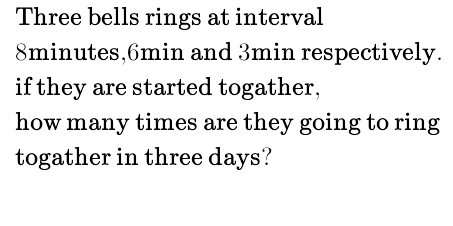
Commented by mondodotto@gmail.com last updated on 21/Mar/18

$$\:\mathrm{help} \\ $$
Answered by MJS last updated on 21/Mar/18
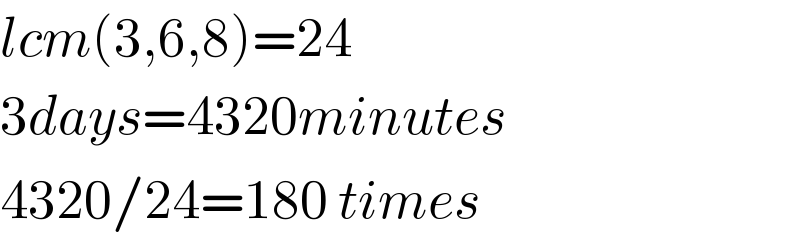
$${lcm}\left(\mathrm{3},\mathrm{6},\mathrm{8}\right)=\mathrm{24} \\ $$$$\mathrm{3}{days}=\mathrm{4320}{minutes} \\ $$$$\mathrm{4320}/\mathrm{24}=\mathrm{180}\:{times} \\ $$
Commented by mondodotto@gmail.com last updated on 21/Mar/18

$$\mathrm{more}\:\mathrm{explaination}\:\mathrm{please} \\ $$
Commented by mondodotto@gmail.com last updated on 21/Mar/18

$$\mathrm{how}\:\boldsymbol{{lcm}}\:\mathrm{24}? \\ $$
Commented by MJS last updated on 21/Mar/18

$$\mathrm{1}^{{st}} \:{bell} \\ $$$$\mathrm{0}\:\mathrm{8}\:\mathrm{16}\:\mathrm{24}\:\mathrm{32}… \\ $$$$\mathrm{2}^{{nd}} \:{bell} \\ $$$$\mathrm{0}\:\mathrm{6}\:\mathrm{12}\:\mathrm{18}\:\mathrm{24}\:\mathrm{30}… \\ $$$$\mathrm{3}^{{rd}} \:{bell} \\ $$$$\mathrm{0}\:\mathrm{3}\:\mathrm{6}\:\mathrm{9}\:\mathrm{12}\:\mathrm{15}\:\mathrm{18}\:\mathrm{21}\:\mathrm{24}\:\mathrm{27}… \\ $$
Commented by mondodotto@gmail.com last updated on 22/Mar/18
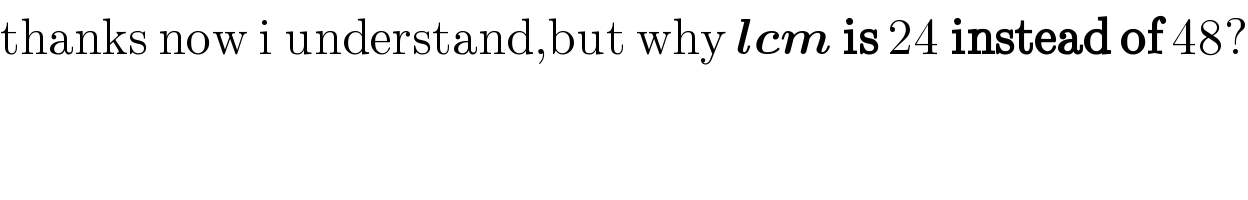
$$\mathrm{thanks}\:\mathrm{now}\:\mathrm{i}\:\mathrm{understand},\mathrm{but}\:\mathrm{why}\:\boldsymbol{{lcm}}\:\boldsymbol{\mathrm{is}}\:\mathrm{24}\:\boldsymbol{\mathrm{instead}}\:\boldsymbol{\mathrm{of}}\:\mathrm{48}? \\ $$
Commented by Joel578 last updated on 22/Mar/18
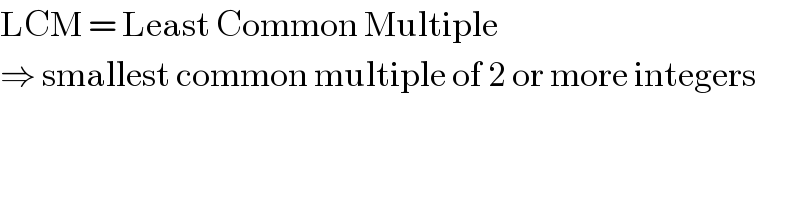
$$\mathrm{LCM}\:=\:\mathrm{Least}\:\mathrm{Common}\:\mathrm{Multiple} \\ $$$$\Rightarrow\:\mathrm{smallest}\:\mathrm{common}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{2}\:\mathrm{or}\:\mathrm{more}\:\mathrm{integers} \\ $$
Commented by MJS last updated on 22/Mar/18

$$\mathrm{8}=\mathrm{2}×\mathrm{2}×\mathrm{2}=\mathrm{2}^{\mathrm{3}} \\ $$$$\mathrm{6}=\mathrm{2}×\mathrm{3}=\mathrm{2}^{\mathrm{1}} ×\mathrm{3}^{\mathrm{1}} \\ $$$$\mathrm{3}=\mathrm{3}^{\mathrm{1}} \\ $$$$\mathrm{for}\:\mathrm{the}\:{lcm}\:\mathrm{you}\:\mathrm{need}\:\mathrm{all}\:\mathrm{prime} \\ $$$$\mathrm{factors}\:\mathrm{of}\:\mathrm{the}\:\mathrm{highest}\:\mathrm{power}, \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{1}} =\mathrm{24} \\ $$$$\mathrm{example}:\:{lcm}\left(\mathrm{42},\mathrm{45},\mathrm{48}\right)=\mathrm{5040} \\ $$$$\mathrm{42}=\mathrm{2}^{\mathrm{1}} ×\mathrm{3}^{\mathrm{1}} ×\mathrm{7}^{\mathrm{1}} \\ $$$$\mathrm{45}=\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{1}} \\ $$$$\mathrm{48}=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{1}} \\ $$$$\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{1}} ×\mathrm{7}^{\mathrm{1}} =\mathrm{5040} \\ $$$$ \\ $$$${lcm}\:\mathrm{of}\:\mathrm{prime}\:\mathrm{numbers}\:{p}_{\mathrm{1}} ,\:{p}_{\mathrm{2}} …{p}_{{n}} = \\ $$$$={p}_{\mathrm{1}} ×{p}_{\mathrm{2}} ×…×{p}_{{n}} \\ $$$${lcm}\left({a},{b}\right)\:\mathrm{with}\:{a}\mid{b}\:\mathrm{is}\:{b} \\ $$$$\mathrm{i}.\mathrm{e}.:\:{lcm}\left(\mathrm{7},\mathrm{21}\right)=\mathrm{21};\:{lcm}\left(\mathrm{2},\mathrm{6},\mathrm{12}\right)=\mathrm{12} \\ $$
