Question Number 32240 by mondodotto@gmail.com last updated on 22/Mar/18
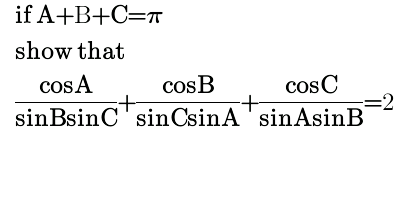
Answered by MJS last updated on 22/Mar/18
![((cos α)/(sin β×sin γ))+((cos β)/(sin α×sin γ))+((cos γ)/(sin α×sin β))= =((cos α×sin α+cos β×sin β+cos γ×sin γ)/(sin α×sin β×sin γ)) I. cos α×sin α+cos β×sin β+cos γ×sin γ= [using cos θ×sin θ=((sin 2θ)/2)] =((sin 2α+sin 2β+sin 2γ)/2) with γ=π−(α+β) and sin 2(π−(α+β))=sin(2π−(2α+2β))= =−sin(2α+2β) this becomes ((sin 2α+sin 2β−sin(2α+2β))/2)=Z/2 II. sin α×sin β×sin γ with γ=π−(α+β) and sin(π−(α+β))=sin(α+β) this becomes sin α×sin β×sin(α+β)= =sin α×sin β×(cos α×sin β+sin α×cos β)= =sin α×cos α×sin^2 β+sin β×cos β×sin^2 α= [using sin^2 θ=((1−cos 2θ)/2)] =((sin 2α)/2)×((1−cos 2β)/2)+((sin 2β)/2)×((1−cos 2α)/2)= =((sin 2α−sin 2α×cos 2β+sin 2β−sin 2β×cos 2α)/4)= [using sin θ×cos φ=((sin(θ−φ)+sin(θ+φ))/2)] =((sin 2α−((sin(2α−2β)+sin(2α+2β))/2)+sin 2β−((sin(2β−2α)+sin(2β+2α))/2))/4)= =((sin 2α+sin 2β−((sin(2α−2β)+sin(2α+2β)−sin(2α−2β)+sin(2α+2β))/2))/4)= =((sin 2α+sin 2β−sin(2α+2β))/4) =((sin 2α+sin 2β−sin(2α+2β))/4)=Z/4 ((Z/2)/(Z/4))=2](https://www.tinkutara.com/question/Q32310.png)
$$\frac{\mathrm{cos}\:\alpha}{\mathrm{sin}\:\beta×\mathrm{sin}\:\gamma}+\frac{\mathrm{cos}\:\beta}{\mathrm{sin}\:\alpha×\mathrm{sin}\:\gamma}+\frac{\mathrm{cos}\:\gamma}{\mathrm{sin}\:\alpha×\mathrm{sin}\:\beta}= \\ $$$$=\frac{\mathrm{cos}\:\alpha×\mathrm{sin}\:\alpha+\mathrm{cos}\:\beta×\mathrm{sin}\:\beta+\mathrm{cos}\:\gamma×\mathrm{sin}\:\gamma}{\mathrm{sin}\:\alpha×\mathrm{sin}\:\beta×\mathrm{sin}\:\gamma} \\ $$$$ \\ $$$$\mathrm{I}. \\ $$$$\mathrm{cos}\:\alpha×\mathrm{sin}\:\alpha+\mathrm{cos}\:\beta×\mathrm{sin}\:\beta+\mathrm{cos}\:\gamma×\mathrm{sin}\:\gamma= \\ $$$$\:\:\:\:\:\left[\mathrm{using}\:\mathrm{cos}\:\theta×\mathrm{sin}\:\theta=\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{sin}\:\mathrm{2}\alpha+\mathrm{sin}\:\mathrm{2}\beta+\mathrm{sin}\:\mathrm{2}\gamma}{\mathrm{2}} \\ $$$$\mathrm{with}\:\gamma=\pi−\left(\alpha+\beta\right)\:\mathrm{and} \\ $$$$\mathrm{sin}\:\mathrm{2}\left(\pi−\left(\alpha+\beta\right)\right)=\mathrm{sin}\left(\mathrm{2}\pi−\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)\right)= \\ $$$$=−\mathrm{sin}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)\:\mathrm{this}\:\mathrm{becomes} \\ $$$$\frac{\mathrm{sin}\:\mathrm{2}\alpha+\mathrm{sin}\:\mathrm{2}\beta−\mathrm{sin}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)}{\mathrm{2}}={Z}/\mathrm{2} \\ $$$$ \\ $$$$\mathrm{II}. \\ $$$$\mathrm{sin}\:\alpha×\mathrm{sin}\:\beta×\mathrm{sin}\:\gamma \\ $$$$\mathrm{with}\:\gamma=\pi−\left(\alpha+\beta\right)\:\mathrm{and} \\ $$$$\mathrm{sin}\left(\pi−\left(\alpha+\beta\right)\right)=\mathrm{sin}\left(\alpha+\beta\right)\:\mathrm{this} \\ $$$$\mathrm{becomes} \\ $$$$\mathrm{sin}\:\alpha×\mathrm{sin}\:\beta×\mathrm{sin}\left(\alpha+\beta\right)= \\ $$$$=\mathrm{sin}\:\alpha×\mathrm{sin}\:\beta×\left(\mathrm{cos}\:\alpha×\mathrm{sin}\:\beta+\mathrm{sin}\:\alpha×\mathrm{cos}\:\beta\right)= \\ $$$$=\mathrm{sin}\:\alpha×\mathrm{cos}\:\alpha×\mathrm{sin}^{\mathrm{2}} \beta+\mathrm{sin}\:\beta×\mathrm{cos}\:\beta×\mathrm{sin}^{\mathrm{2}} \alpha= \\ $$$$\:\:\:\:\:\left[\mathrm{using}\:\mathrm{sin}^{\mathrm{2}} \theta=\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{2}}×\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\beta}{\mathrm{2}}+\frac{\mathrm{sin}\:\mathrm{2}\beta}{\mathrm{2}}×\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\alpha}{\mathrm{2}}= \\ $$$$=\frac{\mathrm{sin}\:\mathrm{2}\alpha−\mathrm{sin}\:\mathrm{2}\alpha×\mathrm{cos}\:\mathrm{2}\beta+\mathrm{sin}\:\mathrm{2}\beta−\mathrm{sin}\:\mathrm{2}\beta×\mathrm{cos}\:\mathrm{2}\alpha}{\mathrm{4}}= \\ $$$$\:\:\:\:\:\left[\mathrm{using}\:\mathrm{sin}\:\theta×\mathrm{cos}\:\phi=\frac{\mathrm{sin}\left(\theta−\phi\right)+\mathrm{sin}\left(\theta+\phi\right)}{\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{sin}\:\mathrm{2}\alpha−\frac{\mathrm{sin}\left(\mathrm{2}\alpha−\mathrm{2}\beta\right)+\mathrm{sin}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)}{\mathrm{2}}+\mathrm{sin}\:\mathrm{2}\beta−\frac{\mathrm{sin}\left(\mathrm{2}\beta−\mathrm{2}\alpha\right)+\mathrm{sin}\left(\mathrm{2}\beta+\mathrm{2}\alpha\right)}{\mathrm{2}}}{\mathrm{4}}= \\ $$$$=\frac{\mathrm{sin}\:\mathrm{2}\alpha+\mathrm{sin}\:\mathrm{2}\beta−\frac{\mathrm{sin}\left(\mathrm{2}\alpha−\mathrm{2}\beta\right)+\mathrm{sin}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)−\mathrm{sin}\left(\mathrm{2}\alpha−\mathrm{2}\beta\right)+\mathrm{sin}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)}{\mathrm{2}}}{\mathrm{4}}= \\ $$$$=\frac{\mathrm{sin}\:\mathrm{2}\alpha+\mathrm{sin}\:\mathrm{2}\beta−\mathrm{sin}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)}{\mathrm{4}} \\ $$$$=\frac{\mathrm{sin}\:\mathrm{2}\alpha+\mathrm{sin}\:\mathrm{2}\beta−\mathrm{sin}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)}{\mathrm{4}}={Z}/\mathrm{4} \\ $$$$ \\ $$$$\frac{{Z}/\mathrm{2}}{{Z}/\mathrm{4}}=\mathrm{2} \\ $$
Commented by mondodotto@gmail.com last updated on 23/Mar/18
$$\mathrm{thanx}\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{this} \\ $$
