Question Number 32379 by mondodotto@gmail.com last updated on 24/Mar/18

Answered by MJS last updated on 24/Mar/18
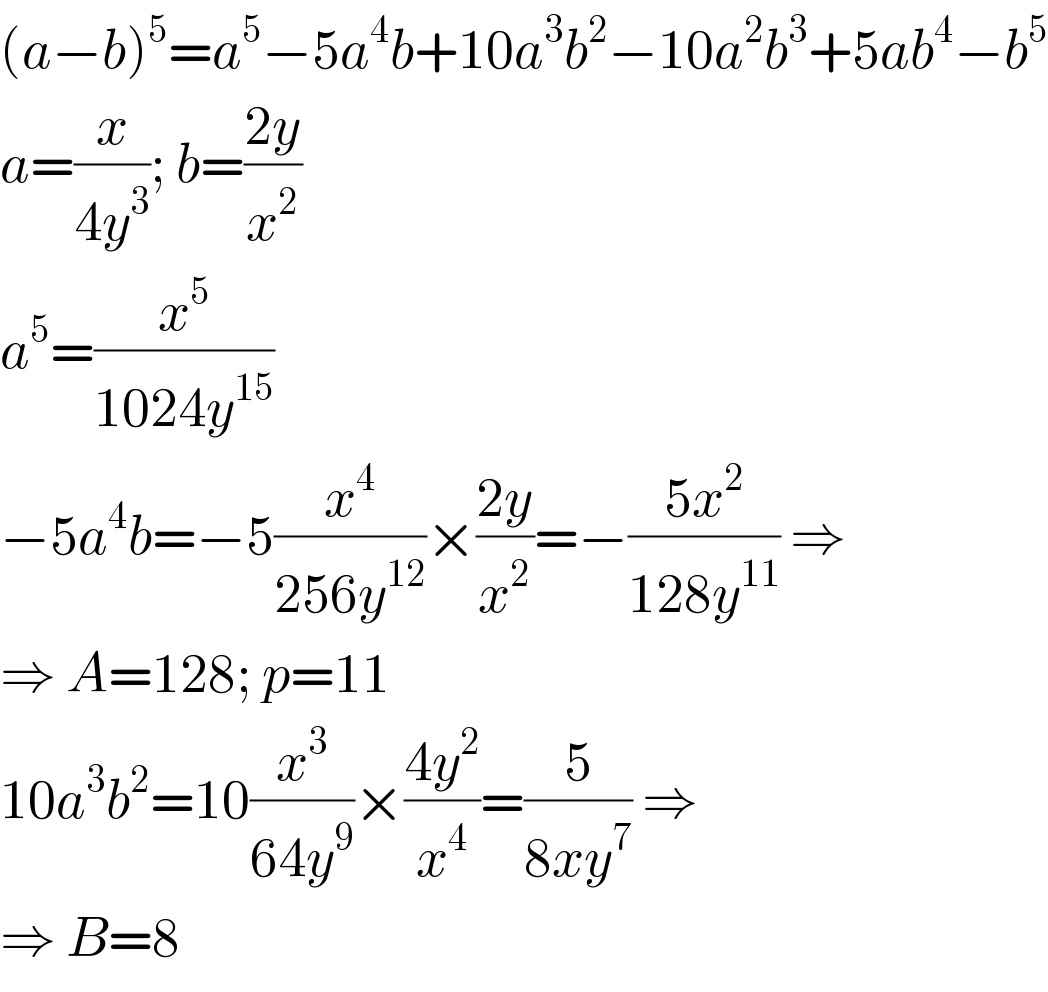
$$\left({a}−{b}\right)^{\mathrm{5}} ={a}^{\mathrm{5}} −\mathrm{5}{a}^{\mathrm{4}} {b}+\mathrm{10}{a}^{\mathrm{3}} {b}^{\mathrm{2}} −\mathrm{10}{a}^{\mathrm{2}} {b}^{\mathrm{3}} +\mathrm{5}{ab}^{\mathrm{4}} −{b}^{\mathrm{5}} \\ $$$${a}=\frac{{x}}{\mathrm{4}{y}^{\mathrm{3}} };\:{b}=\frac{\mathrm{2}{y}}{{x}^{\mathrm{2}} } \\ $$$${a}^{\mathrm{5}} =\frac{{x}^{\mathrm{5}} }{\mathrm{1024}{y}^{\mathrm{15}} } \\ $$$$−\mathrm{5}{a}^{\mathrm{4}} {b}=−\mathrm{5}\frac{{x}^{\mathrm{4}} }{\mathrm{256}{y}^{\mathrm{12}} }×\frac{\mathrm{2}{y}}{{x}^{\mathrm{2}} }=−\frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{128}{y}^{\mathrm{11}} }\:\Rightarrow \\ $$$$\Rightarrow\:{A}=\mathrm{128};\:{p}=\mathrm{11} \\ $$$$\mathrm{10}{a}^{\mathrm{3}} {b}^{\mathrm{2}} =\mathrm{10}\frac{{x}^{\mathrm{3}} }{\mathrm{64}{y}^{\mathrm{9}} }×\frac{\mathrm{4}{y}^{\mathrm{2}} }{{x}^{\mathrm{4}} }=\frac{\mathrm{5}}{\mathrm{8}{xy}^{\mathrm{7}} }\:\Rightarrow \\ $$$$\Rightarrow\:{B}=\mathrm{8} \\ $$
Commented by mondodotto@gmail.com last updated on 24/Mar/18

$$\mathrm{thanx} \\ $$
