Question Number 32380 by mondodotto@gmail.com last updated on 24/Mar/18
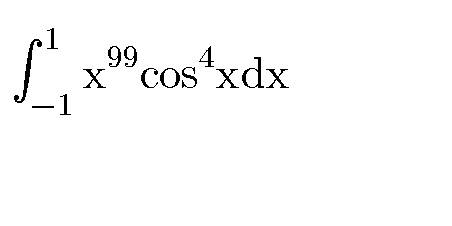
Commented by prof Abdo imad last updated on 24/Mar/18
![let prove if f is odd and imtegrable in[−a,a] ∫_(−a) ^a f(x)dx=0 we have ∫_(−a) ^a f(x)dx= ∫_(−a) ^0 f(x)dx +∫_0 ^a f(x)dx ch.x=−t give ∫_(−a) ^0 f(x)dx= ∫_a ^0 f(−t)(−dt) = ∫_a ^0 f(t)dt =−∫_0 ^a f(t)dt ⇒ ∫_(−a) ^a f(x)dx= −∫_0 ^a f(x)dx +∫_0 ^a f(x)dx =0](https://www.tinkutara.com/question/Q32421.png)
$${let}\:{prove}\:{if}\:{f}\:{is}\:{odd}\:{and}\:{imtegrable}\:{in}\left[−{a},{a}\right] \\ $$$$\int_{−{a}} ^{{a}} {f}\left({x}\right){dx}=\mathrm{0}\:{we}\:{have}\: \\ $$$$\int_{−{a}} ^{{a}} \:{f}\left({x}\right){dx}=\:\int_{−{a}} ^{\mathrm{0}} {f}\left({x}\right){dx}\:+\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}\:{ch}.{x}=−{t} \\ $$$${give}\:\int_{−{a}} ^{\mathrm{0}} {f}\left({x}\right){dx}=\:\int_{{a}} ^{\mathrm{0}} \:{f}\left(−{t}\right)\left(−{dt}\right) \\ $$$$=\:\int_{{a}} ^{\mathrm{0}} {f}\left({t}\right){dt}\:=−\int_{\mathrm{0}} ^{{a}} \:{f}\left({t}\right){dt}\:\Rightarrow \\ $$$$\int_{−{a}} ^{{a}} {f}\left({x}\right){dx}=\:−\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}\:+\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}\:=\mathrm{0} \\ $$
Commented by prof Abdo imad last updated on 24/Mar/18
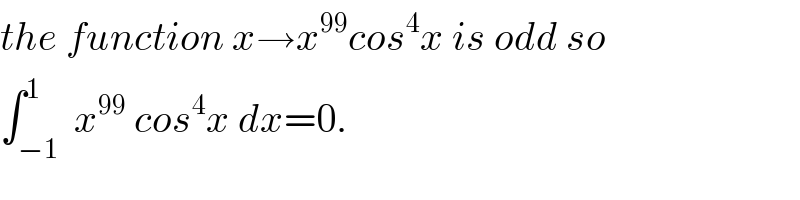
$${the}\:{function}\:{x}\rightarrow{x}^{\mathrm{99}} {cos}^{\mathrm{4}} {x}\:{is}\:{odd}\:{so} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} \:{x}^{\mathrm{99}} \:{cos}^{\mathrm{4}} {x}\:{dx}=\mathrm{0}. \\ $$
Answered by Joel578 last updated on 24/Mar/18
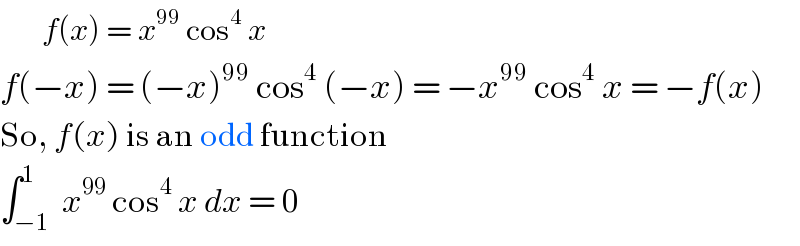
$$\:\:\:\:\:\:\:{f}\left({x}\right)\:=\:{x}^{\mathrm{99}} \:\mathrm{cos}^{\mathrm{4}} \:{x} \\ $$$${f}\left(−{x}\right)\:=\:\left(−{x}\right)^{\mathrm{99}} \:\mathrm{cos}^{\mathrm{4}} \:\left(−{x}\right)\:=\:−{x}^{\mathrm{99}} \:\mathrm{cos}^{\mathrm{4}} \:{x}\:=\:−{f}\left({x}\right) \\ $$$$\mathrm{So},\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{function}\: \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} \:{x}^{\mathrm{99}} \:\mathrm{cos}^{\mathrm{4}} \:{x}\:{dx}\:=\:\mathrm{0} \\ $$
Commented by mondodotto@gmail.com last updated on 24/Mar/18

$$\mathrm{how}? \\ $$
Commented by Joel578 last updated on 24/Mar/18
$$\mathrm{Sorry},\:\mathrm{it}'\mathrm{s}\:\mathrm{corrected}\:\mathrm{now}.\:\mathrm{Thank}\:\mathrm{you} \\ $$
Commented by MJS last updated on 24/Mar/18
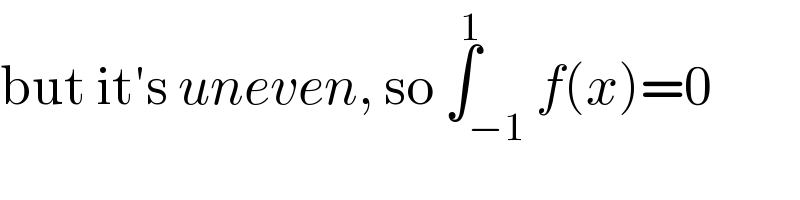
$$\mathrm{but}\:\mathrm{it}'\mathrm{s}\:{uneven},\:\mathrm{so}\:\overset{\mathrm{1}} {\int}_{−\mathrm{1}} {f}\left({x}\right)=\mathrm{0} \\ $$
Commented by MJS last updated on 24/Mar/18
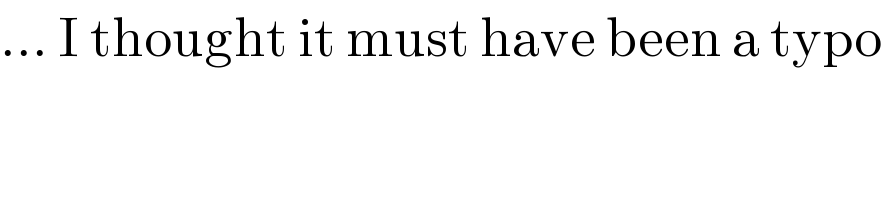
$$…\:\mathrm{I}\:\mathrm{thought}\:\mathrm{it}\:\mathrm{must}\:\mathrm{have}\:\mathrm{been}\:\mathrm{a}\:\mathrm{typo} \\ $$
