Question Number 32446 by Mr eaay last updated on 25/Mar/18
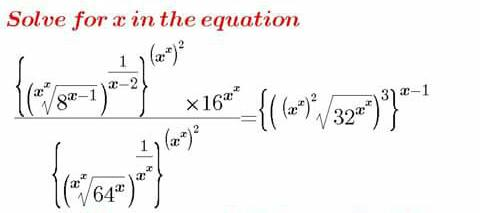
Answered by MJS last updated on 25/Mar/18

$$\mathrm{left}\:\mathrm{side}: \\ $$$$\mathrm{8}^{\frac{\left({x}−\mathrm{1}\right){x}^{\mathrm{2}{x}} }{{x}^{{x}} \left({x}−\mathrm{2}\right)}} ×\mathrm{16}^{{x}^{{x}} } =\mathrm{8}^{\frac{\left({x}−\mathrm{1}\right){x}^{{x}} }{{x}−\mathrm{2}}} ×\mathrm{8}^{\frac{\mathrm{4}{x}^{{x}} }{\mathrm{3}}} = \\ $$$$=\mathrm{8}^{\left(\frac{\mathrm{1}}{{x}−\mathrm{2}}+\frac{\mathrm{7}}{\mathrm{3}}\right){x}^{{x}} } =\mathrm{2}^{\left(\frac{\mathrm{3}}{{x}−\mathrm{2}}+\mathrm{7}\right){x}^{{x}} } \\ $$$$\mathrm{64}^{\frac{{x}×{x}^{\mathrm{2}{x}} }{{x}^{{x}} ×{x}^{{x}} }} =\mathrm{64}^{{x}} =\mathrm{2}^{\mathrm{6}{x}} \\ $$$$\mathrm{left}\:\mathrm{side}=\mathrm{2}^{\left(\frac{\mathrm{3}}{{x}−\mathrm{2}}+\mathrm{7}\right){x}^{{x}} −\mathrm{6}{x}} \\ $$$$ \\ $$$$\mathrm{right}\:\mathrm{side}: \\ $$$$\mathrm{32}^{\frac{\mathrm{3}\left({x}−\mathrm{1}\right){x}^{{x}} }{{x}^{\mathrm{2}{x}} }} =\mathrm{32}^{\frac{\mathrm{3}\left({x}−\mathrm{1}\right)}{{x}^{{x}} }} =\mathrm{2}^{\frac{\mathrm{15}\left({x}−\mathrm{1}\right)}{{x}^{{x}} }} \\ $$$$ \\ $$$$\left(\frac{\mathrm{3}}{{x}−\mathrm{2}}+\mathrm{7}\right){x}^{{x}} −\mathrm{6}{x}=\frac{\mathrm{15}\left({x}−\mathrm{1}\right)}{{x}^{{x}} } \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved} \\ $$$$\mathrm{exactly}.\:\mathrm{By}\:\mathrm{trying}\:\mathrm{I}\:\mathrm{found} \\ $$$${x}\approx.\mathrm{90597422346646} \\ $$
