Question-32534

Question Number 32534 by naka3546 last updated on 27/Mar/18

Answered by MJS last updated on 27/Mar/18

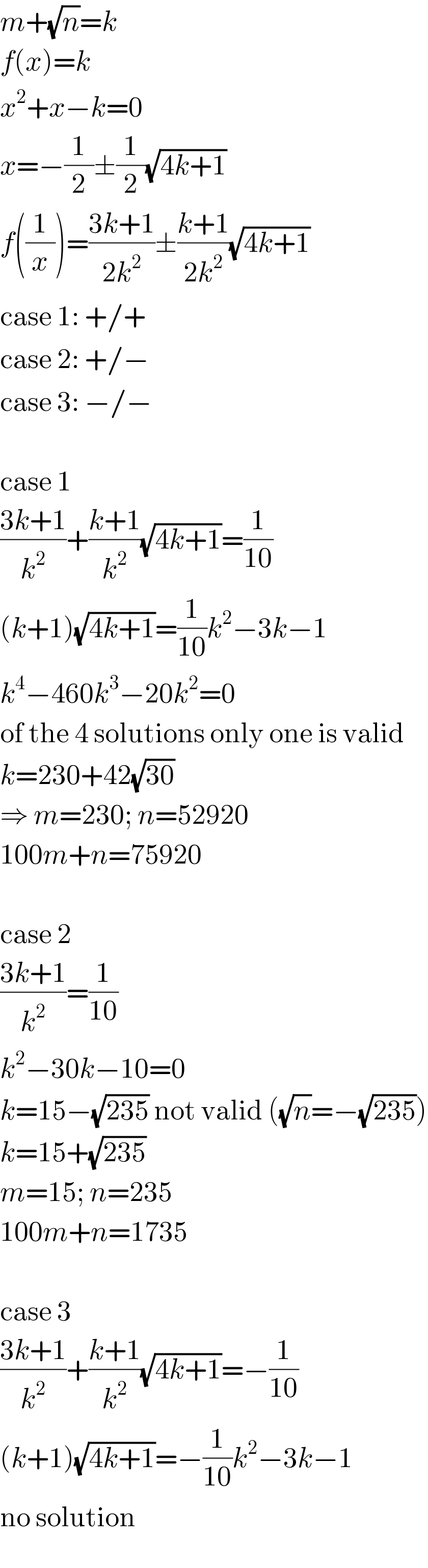
m+(√n)=k f(x)=k x^2 +x−k=0 x=−(1/2)±(1/2)(√(4k+1)) f((1/x))=((3k+1)/(2k^2 ))±((k+1)/(2k^2 ))(√(4k+1)) case 1: +/+ case 2: +/− case 3: −/− case 1 ((3k+1)/k^2 )+((k+1)/k^2 )(√(4k+1))=(1/(10)) (k+1)(√(4k+1))=(1/(10))k^2 −3k−1 k^4 −460k^3 −20k^2 =0 of the 4 solutions only one is valid k=230+42(√(30)) ⇒ m=230; n=52920 100m+n=75920 case 2 ((3k+1)/k^2 )=(1/(10)) k^2 −30k−10=0 k=15−(√(235)) not valid ((√n)=−(√(235))) k=15+(√(235)) m=15; n=235 100m+n=1735 case 3 ((3k+1)/k^2 )+((k+1)/k^2 )(√(4k+1))=−(1/(10)) (k+1)(√(4k+1))=−(1/(10))k^2 −3k−1 no solution

$${m}+\sqrt{{n}}={k} \\ $$$${f}\left({x}\right)={k} \\ $$$${x}^{\mathrm{2}} +{x}−{k}=\mathrm{0} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{4}{k}+\mathrm{1}} \\ $$$${f}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\mathrm{3}{k}+\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} }\pm\frac{{k}+\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} }\sqrt{\mathrm{4}{k}+\mathrm{1}} \\ $$$$\mathrm{case}\:\mathrm{1}:\:+/+ \\ $$$$\mathrm{case}\:\mathrm{2}:\:+/− \\ $$$$\mathrm{case}\:\mathrm{3}:\:−/− \\ $$$$ \\ $$$$\mathrm{case}\:\mathrm{1} \\ $$$$\frac{\mathrm{3}{k}+\mathrm{1}}{{k}^{\mathrm{2}} }+\frac{{k}+\mathrm{1}}{{k}^{\mathrm{2}} }\sqrt{\mathrm{4}{k}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$$\left({k}+\mathrm{1}\right)\sqrt{\mathrm{4}{k}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{10}}{k}^{\mathrm{2}} −\mathrm{3}{k}−\mathrm{1} \\ $$$${k}^{\mathrm{4}} −\mathrm{460}{k}^{\mathrm{3}} −\mathrm{20}{k}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{4}\:\mathrm{solutions}\:\mathrm{only}\:\mathrm{one}\:\mathrm{is}\:\mathrm{valid} \\ $$$${k}=\mathrm{230}+\mathrm{42}\sqrt{\mathrm{30}} \\ $$$$\Rightarrow\:{m}=\mathrm{230};\:{n}=\mathrm{52920} \\ $$$$\mathrm{100}{m}+{n}=\mathrm{75920} \\ $$$$ \\ $$$$\mathrm{case}\:\mathrm{2} \\ $$$$\frac{\mathrm{3}{k}+\mathrm{1}}{{k}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${k}^{\mathrm{2}} −\mathrm{30}{k}−\mathrm{10}=\mathrm{0} \\ $$$${k}=\mathrm{15}−\sqrt{\mathrm{235}}\:\mathrm{not}\:\mathrm{valid}\:\left(\sqrt{{n}}=−\sqrt{\mathrm{235}}\right) \\ $$$${k}=\mathrm{15}+\sqrt{\mathrm{235}} \\ $$$${m}=\mathrm{15};\:{n}=\mathrm{235} \\ $$$$\mathrm{100}{m}+{n}=\mathrm{1735} \\ $$$$ \\ $$$$\mathrm{case}\:\mathrm{3} \\ $$$$\frac{\mathrm{3}{k}+\mathrm{1}}{{k}^{\mathrm{2}} }+\frac{{k}+\mathrm{1}}{{k}^{\mathrm{2}} }\sqrt{\mathrm{4}{k}+\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{10}} \\ $$$$\left({k}+\mathrm{1}\right)\sqrt{\mathrm{4}{k}+\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{10}}{k}^{\mathrm{2}} −\mathrm{3}{k}−\mathrm{1} \\ $$$$\mathrm{no}\:\mathrm{solution} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply