Question Number 32538 by GAUTHAM last updated on 27/Mar/18
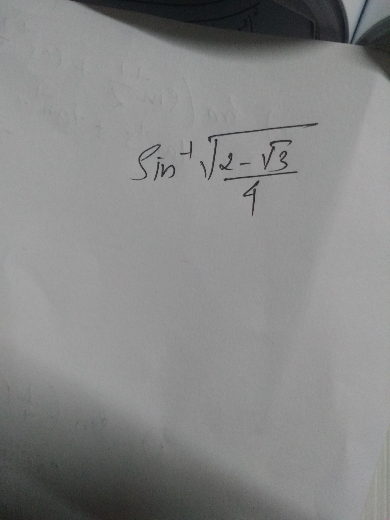
Commented by prof Abdo imad last updated on 28/Mar/18
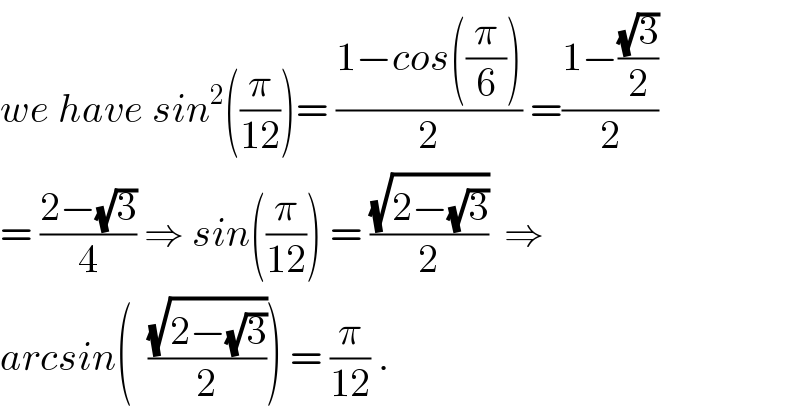
$${we}\:{have}\:{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}\right)=\:\frac{\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{6}}\right)}{\mathrm{2}}\:=\frac{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{4}}\:\Rightarrow\:{sin}\left(\frac{\pi}{\mathrm{12}}\right)\:=\:\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}\:\:\Rightarrow \\ $$$${arcsin}\left(\:\:\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}\right)\:=\:\frac{\pi}{\mathrm{12}}\:. \\ $$
Answered by rahul 19 last updated on 27/Mar/18

$$\mathrm{sin}^{−\mathrm{1}} \:\sqrt{\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{4}}} \\ $$$$\Rightarrow\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\:\mathrm{15}° \\ $$
Commented by MJS last updated on 27/Mar/18
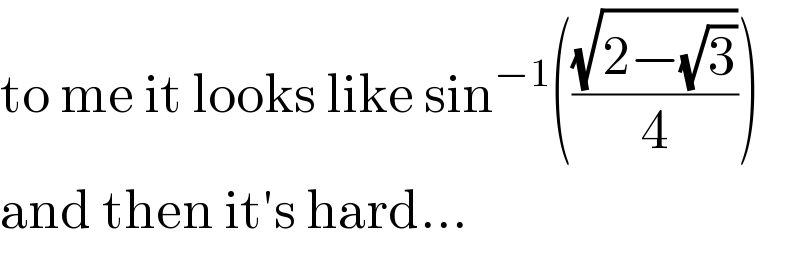
$$\mathrm{to}\:\mathrm{me}\:\mathrm{it}\:\mathrm{looks}\:\mathrm{like}\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{4}}\right) \\ $$$$\mathrm{and}\:\mathrm{then}\:\mathrm{it}'\mathrm{s}\:\mathrm{hard}… \\ $$
Commented by rahul 19 last updated on 27/Mar/18
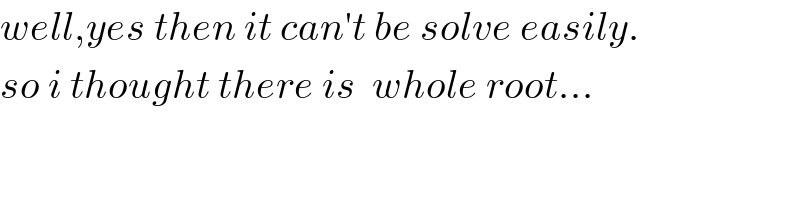
$${well},{yes}\:{then}\:{it}\:{can}'{t}\:{be}\:{solve}\:{easily}. \\ $$$${so}\:{i}\:{thought}\:{there}\:{is}\:\:{whole}\:{root}… \\ $$
