Menu Close

Question-32666

Tinku Tara 0 Comments
Pin




Question Number 32666 by naka3546 last updated on 30/Mar/18
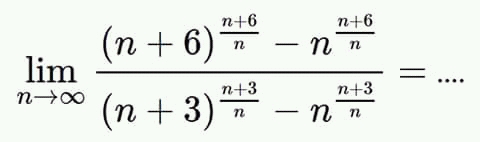
Commented by abdo imad last updated on 30/Mar/18
let put A_n = (((n+6)^((n+6)/n) −n^((n+6)/n) )/((n+3)^((n+3)/n) − n^((n+3)/n) )) A_n =((n^((n+6)/n) ( (1 +(6/n))^((n+6)/n) −1))/(n^((n+3)/n) ( (1+(3/n))^((n+3)/n) −1))) =n^(3/n) (((1 +(6/n))^((n+6)/n) −1)/((1+(3/n))^((n+3)/n) −1)) but (1+(6/n))^((n+6)/n) ∼ 1+ ((6(n+6))/n^2 ) ⇒(1+(6/n))^((n+6)/n) −1 ∼ ((6(n+6))/n^2 ) (1+(3/n))^((n+3)/n) ∼ 1+ ((3(n+3))/n^2 ) ⇒ (1+(3/n))^((n+3)/n) −1 ∼ ((3(n+3))/n^2 ) ⇒ A_n ∼ n^(3/n) ((6n+36)/(3n +9)) ⇒ A_n ∼2 e_(n→∞) ^((3/n)ln(n)) → 2 so lim_(n→∞) A_n =2 .
$${let}\:{put}\:{A}_{{n}} =\:\frac{\left({n}+\mathrm{6}\right)^{\frac{{n}+\mathrm{6}}{{n}}} \:−{n}^{\frac{{n}+\mathrm{6}}{{n}}} }{\left({n}+\mathrm{3}\right)^{\frac{{n}+\mathrm{3}}{{n}}} \:−\:{n}^{\frac{{n}+\mathrm{3}}{{n}}} } \\ $$$${A}_{{n}} =\frac{{n}^{\frac{{n}+\mathrm{6}}{{n}}} \:\left(\:\:\left(\mathrm{1}\:+\frac{\mathrm{6}}{{n}}\right)^{\frac{{n}+\mathrm{6}}{{n}}} \:\:−\mathrm{1}\right)}{{n}^{\frac{{n}+\mathrm{3}}{{n}}} \left(\:\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)^{\frac{{n}+\mathrm{3}}{{n}}} \:−\mathrm{1}\right)}\:={n}^{\frac{\mathrm{3}}{{n}}} \:\frac{\left(\mathrm{1}\:+\frac{\mathrm{6}}{{n}}\right)^{\frac{{n}+\mathrm{6}}{{n}}} \:−\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)^{\frac{{n}+\mathrm{3}}{{n}}} \:−\mathrm{1}}\:\:{but} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{6}}{{n}}\right)^{\frac{{n}+\mathrm{6}}{{n}}} \:\:\sim\:\mathrm{1}+\:\frac{\mathrm{6}\left({n}+\mathrm{6}\right)}{{n}^{\mathrm{2}} }\:\Rightarrow\left(\mathrm{1}+\frac{\mathrm{6}}{{n}}\right)^{\frac{{n}+\mathrm{6}}{{n}}} \:−\mathrm{1}\:\sim\:\frac{\mathrm{6}\left({n}+\mathrm{6}\right)}{{n}^{\mathrm{2}} } \\ $$$$\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)^{\frac{{n}+\mathrm{3}}{{n}}} \:\sim\:\:\mathrm{1}+\:\frac{\mathrm{3}\left({n}+\mathrm{3}\right)}{{n}^{\mathrm{2}} }\:\Rightarrow\:\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)^{\frac{{n}+\mathrm{3}}{{n}}} \:−\mathrm{1}\:\sim\:\:\frac{\mathrm{3}\left({n}+\mathrm{3}\right)}{{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{A}_{{n}} \sim\:\:{n}^{\frac{\mathrm{3}}{{n}}} \:\:\:\:\frac{\mathrm{6}{n}+\mathrm{36}}{\mathrm{3}{n}\:+\mathrm{9}}\:\Rightarrow\:{A}_{{n}} \:\sim\mathrm{2}\:{e}_{{n}\rightarrow\infty} ^{\frac{\mathrm{3}}{{n}}{ln}\left({n}\right)} \:\:\rightarrow\:\mathrm{2}\:{so} \\ $$$${lim}_{{n}\rightarrow\infty} \:{A}_{{n}} =\mathrm{2}\:. \\ $$$$ \\ $$$$ \\ $$
Commented by MJS last updated on 31/Mar/18
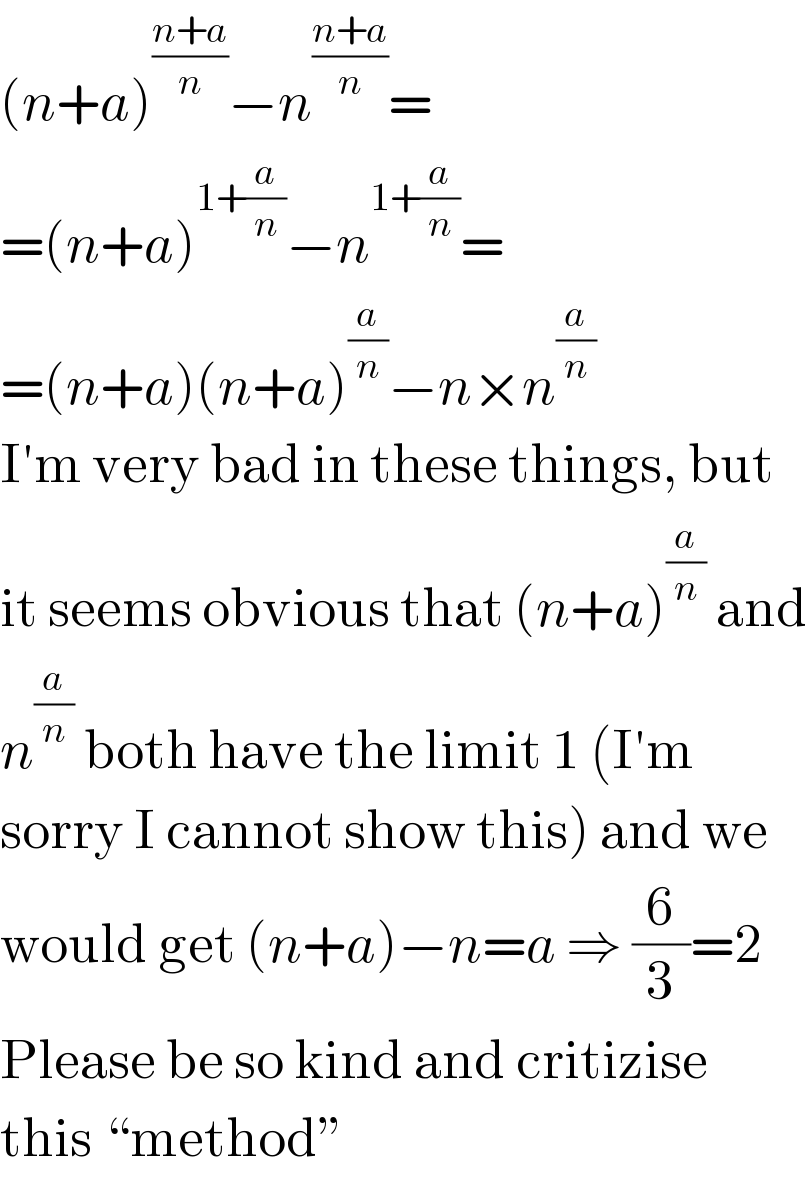
(n+a)^((n+a)/n) −n^((n+a)/n) = =(n+a)^(1+(a/n)) −n^(1+(a/n)) = =(n+a)(n+a)^(a/n) −n×n^(a/n) I′m very bad in these things, but it seems obvious that (n+a)^(a/n) and n^(a/n) both have the limit 1 (I′m sorry I cannot show this) and we would get (n+a)−n=a ⇒ (6/3)=2 Please be so kind and critizise this “method”
$$\left({n}+{a}\right)^{\frac{{n}+{a}}{{n}}} −{n}^{\frac{{n}+{a}}{{n}}} = \\ $$$$=\left({n}+{a}\right)^{\mathrm{1}+\frac{{a}}{{n}}} −{n}^{\mathrm{1}+\frac{{a}}{{n}}} = \\ $$$$=\left({n}+{a}\right)\left({n}+{a}\right)^{\frac{{a}}{{n}}} −{n}×{n}^{\frac{{a}}{{n}}} \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{very}\:\mathrm{bad}\:\mathrm{in}\:\mathrm{these}\:\mathrm{things},\:\mathrm{but} \\ $$$$\mathrm{it}\:\mathrm{seems}\:\mathrm{obvious}\:\mathrm{that}\:\left({n}+{a}\right)^{\frac{{a}}{{n}}} \:\mathrm{and} \\ $$$${n}^{\frac{{a}}{{n}}} \:\mathrm{both}\:\mathrm{have}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{1}\:\left(\mathrm{I}'\mathrm{m}\right. \\ $$$$\left.\mathrm{sorry}\:\mathrm{I}\:\mathrm{cannot}\:\mathrm{show}\:\mathrm{this}\right)\:\mathrm{and}\:\mathrm{we} \\ $$$$\mathrm{would}\:\mathrm{get}\:\left({n}+{a}\right)−{n}={a}\:\Rightarrow\:\frac{\mathrm{6}}{\mathrm{3}}=\mathrm{2} \\ $$$$\mathrm{Please}\:\mathrm{be}\:\mathrm{so}\:\mathrm{kind}\:\mathrm{and}\:\mathrm{critizise} \\ $$$$\mathrm{this}\:“\mathrm{method}'' \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *