Menu Close

Question-32710

Tinku Tara 0 Comments
Pin




Question Number 32710 by mondodotto@gmail.com last updated on 31/Mar/18
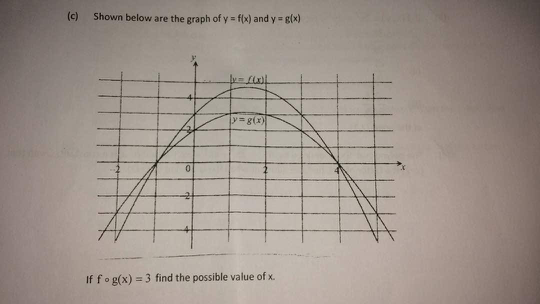
Answered by MJS last updated on 01/Apr/18
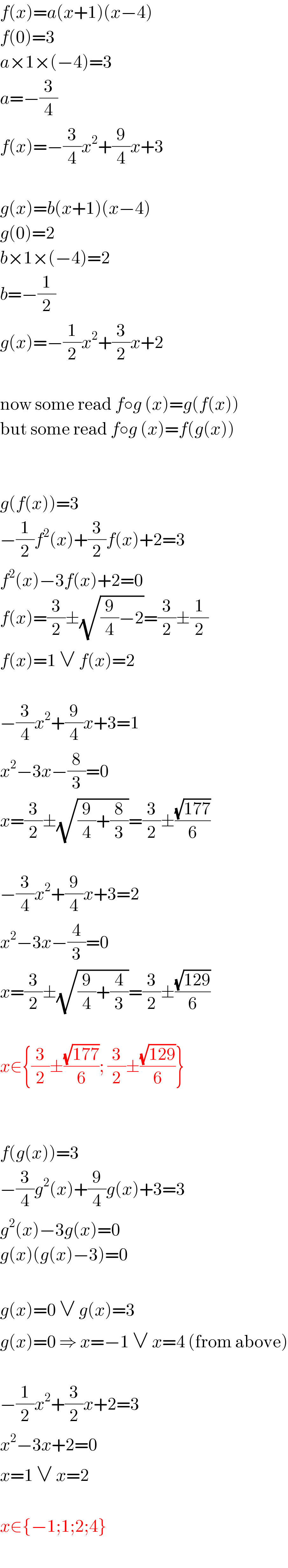
f(x)=a(x+1)(x−4) f(0)=3 a×1×(−4)=3 a=−(3/4) f(x)=−(3/4)x^2 +(9/4)x+3 g(x)=b(x+1)(x−4) g(0)=2 b×1×(−4)=2 b=−(1/2) g(x)=−(1/2)x^2 +(3/2)x+2 now some read f○g (x)=g(f(x)) but some read f○g (x)=f(g(x)) g(f(x))=3 −(1/2)f^2 (x)+(3/2)f(x)+2=3 f^2 (x)−3f(x)+2=0 f(x)=(3/2)±(√((9/4)−2))=(3/2)±(1/2) f(x)=1 ∨ f(x)=2 −(3/4)x^2 +(9/4)x+3=1 x^2 −3x−(8/3)=0 x=(3/2)±(√((9/4)+(8/3)))=(3/2)±((√(177))/6) −(3/4)x^2 +(9/4)x+3=2 x^2 −3x−(4/3)=0 x=(3/2)±(√((9/4)+(4/3)))=(3/2)±((√(129))/6) x∈{(3/2)±((√(177))/6); (3/2)±((√(129))/6)} f(g(x))=3 −(3/4)g^2 (x)+(9/4)g(x)+3=3 g^2 (x)−3g(x)=0 g(x)(g(x)−3)=0 g(x)=0 ∨ g(x)=3 g(x)=0 ⇒ x=−1 ∨ x=4 (from above) −(1/2)x^2 +(3/2)x+2=3 x^2 −3x+2=0 x=1 ∨ x=2 x∈{−1;1;2;4}
$${f}\left({x}\right)={a}\left({x}+\mathrm{1}\right)\left({x}−\mathrm{4}\right) \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{3} \\ $$$${a}×\mathrm{1}×\left(−\mathrm{4}\right)=\mathrm{3} \\ $$$${a}=−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${f}\left({x}\right)=−\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{4}}{x}+\mathrm{3} \\ $$$$ \\ $$$${g}\left({x}\right)={b}\left({x}+\mathrm{1}\right)\left({x}−\mathrm{4}\right) \\ $$$${g}\left(\mathrm{0}\right)=\mathrm{2} \\ $$$${b}×\mathrm{1}×\left(−\mathrm{4}\right)=\mathrm{2} \\ $$$${b}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${g}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}{x}+\mathrm{2} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{some}\:\mathrm{read}\:{f}\circ{g}\:\left({x}\right)={g}\left({f}\left({x}\right)\right) \\ $$$$\mathrm{but}\:\mathrm{some}\:\mathrm{read}\:{f}\circ{g}\:\left({x}\right)={f}\left({g}\left({x}\right)\right) \\ $$$$ \\ $$$$ \\ $$$${g}\left({f}\left({x}\right)\right)=\mathrm{3} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{f}^{\mathrm{2}} \left({x}\right)+\frac{\mathrm{3}}{\mathrm{2}}{f}\left({x}\right)+\mathrm{2}=\mathrm{3} \\ $$$${f}^{\mathrm{2}} \left({x}\right)−\mathrm{3}{f}\left({x}\right)+\mathrm{2}=\mathrm{0} \\ $$$${f}\left({x}\right)=\frac{\mathrm{3}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{9}}{\mathrm{4}}−\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left({x}\right)=\mathrm{1}\:\vee\:{f}\left({x}\right)=\mathrm{2} \\ $$$$ \\ $$$$−\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{4}}{x}+\mathrm{3}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}−\frac{\mathrm{8}}{\mathrm{3}}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{3}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{8}}{\mathrm{3}}}=\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{177}}}{\mathrm{6}} \\ $$$$ \\ $$$$−\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{4}}{x}+\mathrm{3}=\mathrm{2} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}−\frac{\mathrm{4}}{\mathrm{3}}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{3}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{4}}{\mathrm{3}}}=\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{129}}}{\mathrm{6}} \\ $$$$ \\ $$$${x}\in\left\{\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{177}}}{\mathrm{6}};\:\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{129}}}{\mathrm{6}}\right\} \\ $$$$ \\ $$$$ \\ $$$${f}\left({g}\left({x}\right)\right)=\mathrm{3} \\ $$$$−\frac{\mathrm{3}}{\mathrm{4}}{g}^{\mathrm{2}} \left({x}\right)+\frac{\mathrm{9}}{\mathrm{4}}{g}\left({x}\right)+\mathrm{3}=\mathrm{3} \\ $$$${g}^{\mathrm{2}} \left({x}\right)−\mathrm{3}{g}\left({x}\right)=\mathrm{0} \\ $$$${g}\left({x}\right)\left({g}\left({x}\right)−\mathrm{3}\right)=\mathrm{0} \\ $$$$ \\ $$$${g}\left({x}\right)=\mathrm{0}\:\vee\:{g}\left({x}\right)=\mathrm{3} \\ $$$${g}\left({x}\right)=\mathrm{0}\:\Rightarrow\:{x}=−\mathrm{1}\:\vee\:{x}=\mathrm{4}\:\left(\mathrm{from}\:\mathrm{above}\right) \\ $$$$ \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}{x}+\mathrm{2}=\mathrm{3} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}=\mathrm{0} \\ $$$${x}=\mathrm{1}\:\vee\:{x}=\mathrm{2} \\ $$$$ \\ $$$${x}\in\left\{−\mathrm{1};\mathrm{1};\mathrm{2};\mathrm{4}\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *