Question Number 32763 by San Sophanethsan069 last updated on 01/Apr/18
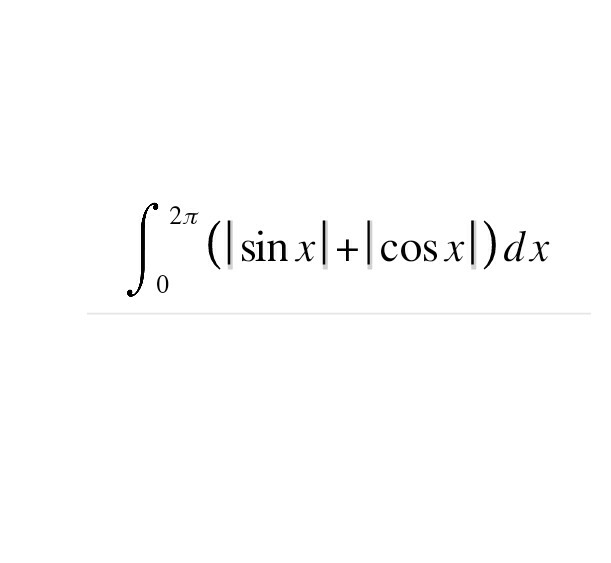
Commented by abdo imad last updated on 01/Apr/18
![let put I = ∫_0 ^(2π) ( ∣sinx∣ +∣cosx∣)dx .ch .x=π +t give I = ∫_(−π) ^π (∣sint∣ +∣cost∣)dt =2 ∫_0 ^π (sint +∣cost∣)dt = 2 ∫_0 ^π sint dt +2 ∫_0 ^π ∣cost∣dt but ∫_0 ^π sint dt =[−cost]_0 ^π = 2 ∫_0 ^π ∣cost∣dt = ∫_0 ^(π/2) cost −∫_(π/2) ^π costdt =[sint]_0 ^(π/2) − [sint]_(π/2) ^π = 1−(−1) =2 ⇒ I = 4 +4 =8 .](https://www.tinkutara.com/question/Q32769.png)
$${let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\:\mid{sinx}\mid\:+\mid{cosx}\mid\right){dx}\:\:.{ch}\:.{x}=\pi\:+{t}\:{give} \\ $$$${I}\:=\:\int_{−\pi} ^{\pi} \:\left(\mid{sint}\mid\:+\mid{cost}\mid\right){dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \:\left({sint}\:+\mid{cost}\mid\right){dt} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \:{sint}\:{dt}\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \:\mid{cost}\mid{dt}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:{sint}\:{dt}\:=\left[−{cost}\right]_{\mathrm{0}} ^{\pi} \:=\:\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\mid{cost}\mid{dt}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cost}\:\:−\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:{costdt} \\ $$$$=\left[{sint}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:−\:\left[{sint}\right]_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:=\:\mathrm{1}−\left(−\mathrm{1}\right)\:=\mathrm{2}\:\Rightarrow \\ $$$${I}\:=\:\mathrm{4}\:+\mathrm{4}\:\:=\mathrm{8}\:\:. \\ $$
Answered by MJS last updated on 02/Apr/18
![sin x, cos x both run a full period in [0;2π] ⇒ ⇒ ∫_0 ^(2π) ∣sin x∣dx = ∫_0 ^(2π) ∣cos x∣dx = = 2∫_0 ^π sin x dx so we′re looking for 4∫_0 ^π sin x dx=−4cos x∣_0 ^π = =−4cos π+4cos 0=8](https://www.tinkutara.com/question/Q32778.png)
$$\mathrm{sin}\:{x},\:\mathrm{cos}\:{x}\:\mathrm{both}\:\mathrm{run}\:\mathrm{a}\:\mathrm{full} \\ $$$$\mathrm{period}\:\mathrm{in}\:\left[\mathrm{0};\mathrm{2}\pi\right]\:\Rightarrow \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\mid\mathrm{sin}\:{x}\mid{dx}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\mid\mathrm{cos}\:{x}\mid{dx}\:= \\ $$$$=\:\mathrm{2}\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{sin}\:{x}\:{dx} \\ $$$$\mathrm{so}\:\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\mathrm{for} \\ $$$$\mathrm{4}\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{sin}\:{x}\:{dx}=−\mathrm{4cos}\:{x}\underset{\mathrm{0}} {\overset{\pi} {\mid}}= \\ $$$$=−\mathrm{4cos}\:\pi+\mathrm{4cos}\:\mathrm{0}=\mathrm{8} \\ $$
