Question Number 32810 by mondodotto@gmail.com last updated on 02/Apr/18
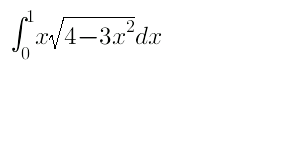
Commented by caravan msup abdo. last updated on 02/Apr/18
![let use the ch. (√3) x =2sint I = ∫_0 ^(π/3) (2/( (√3))) sint (√(4−4sin^2 t)) (2/( (√3))) cost dt I = (8/3) ∫_0 ^(π/3) sint cos^2 t dt = (8/3) [ −(1/3) cos^3 t ]_0 ^(π/3) = −(8/9)( ((1/2))^3 −1) =−(8/9)( (1/8) −1)=−(8/9)(−(7/8))⇒](https://www.tinkutara.com/question/Q32817.png)
$${let}\:{use}\:{the}\:{ch}.\:\sqrt{\mathrm{3}}\:{x}\:=\mathrm{2}{sint} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{sint}\:\sqrt{\mathrm{4}−\mathrm{4}{sin}^{\mathrm{2}} {t}}\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{cost}\:{dt} \\ $$$${I}\:=\:\frac{\mathrm{8}}{\mathrm{3}}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:{sint}\:{cos}^{\mathrm{2}} {t}\:{dt} \\ $$$$=\:\frac{\mathrm{8}}{\mathrm{3}}\:\left[\:−\frac{\mathrm{1}}{\mathrm{3}}\:{cos}^{\mathrm{3}} {t}\:\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \\ $$$$=\:−\frac{\mathrm{8}}{\mathrm{9}}\left(\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} \:−\mathrm{1}\right) \\ $$$$=−\frac{\mathrm{8}}{\mathrm{9}}\left(\:\frac{\mathrm{1}}{\mathrm{8}}\:−\mathrm{1}\right)=−\frac{\mathrm{8}}{\mathrm{9}}\left(−\frac{\mathrm{7}}{\mathrm{8}}\right)\Rightarrow \\ $$
Commented by caravan msup abdo. last updated on 02/Apr/18

$${I}\:=\:\frac{\mathrm{7}}{\mathrm{9}}\:. \\ $$
Answered by Joel578 last updated on 02/Apr/18
![u = 4 − 3x^2 → du = −6x dx I = −(1/6) ∫_4 ^1 (√u) du = −(1/6) [(2/3)u(√u)]_4 ^1 = −(1/6) ((2/3)(√1) − (8/3)(√4))](https://www.tinkutara.com/question/Q32812.png)
$${u}\:=\:\mathrm{4}\:−\:\mathrm{3}{x}^{\mathrm{2}} \:\:\rightarrow\:\:{du}\:=\:−\mathrm{6}{x}\:{dx} \\ $$$${I}\:=\:−\frac{\mathrm{1}}{\mathrm{6}}\:\int_{\mathrm{4}} ^{\mathrm{1}} \:\sqrt{{u}}\:{du} \\ $$$$\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{6}}\:\left[\frac{\mathrm{2}}{\mathrm{3}}{u}\sqrt{{u}}\right]_{\mathrm{4}} ^{\mathrm{1}} \\ $$$$\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{6}}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{1}}\:−\:\frac{\mathrm{8}}{\mathrm{3}}\sqrt{\mathrm{4}}\right) \\ $$
Commented by mondodotto@gmail.com last updated on 02/Apr/18
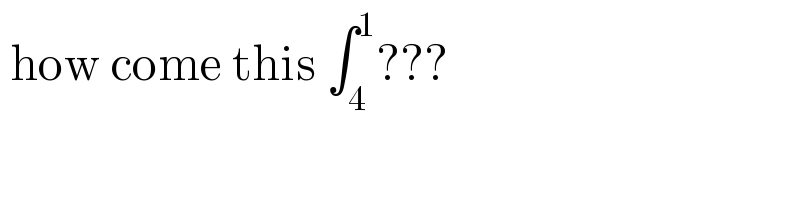
$$\:\mathrm{how}\:\mathrm{come}\:\mathrm{this}\:\int_{\mathrm{4}} ^{\mathrm{1}} ??? \\ $$
Commented by Joel578 last updated on 02/Apr/18
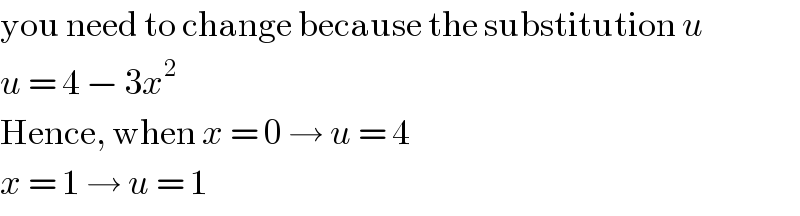
$$\mathrm{you}\:\mathrm{need}\:\mathrm{to}\:\mathrm{change}\:\mathrm{because}\:\mathrm{the}\:\mathrm{substitution}\:{u} \\ $$$${u}\:=\:\mathrm{4}\:−\:\mathrm{3}{x}^{\mathrm{2}} \\ $$$$\mathrm{Hence},\:\mathrm{when}\:{x}\:=\:\mathrm{0}\:\rightarrow\:{u}\:=\:\mathrm{4} \\ $$$${x}\:=\:\mathrm{1}\:\rightarrow\:{u}\:=\:\mathrm{1} \\ $$
