Question-32958

Question Number 32958 by artibunja last updated on 07/Apr/18

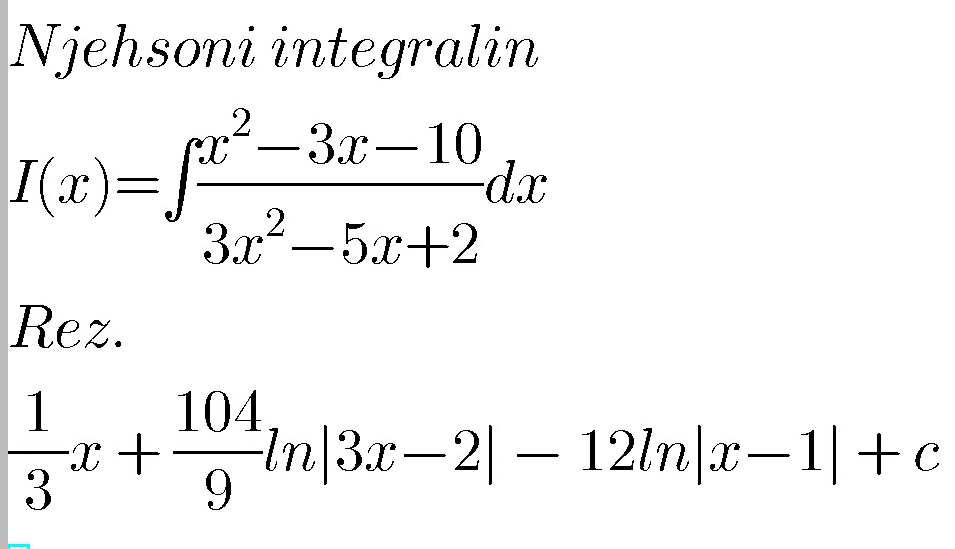
Commented by MJS last updated on 07/Apr/18

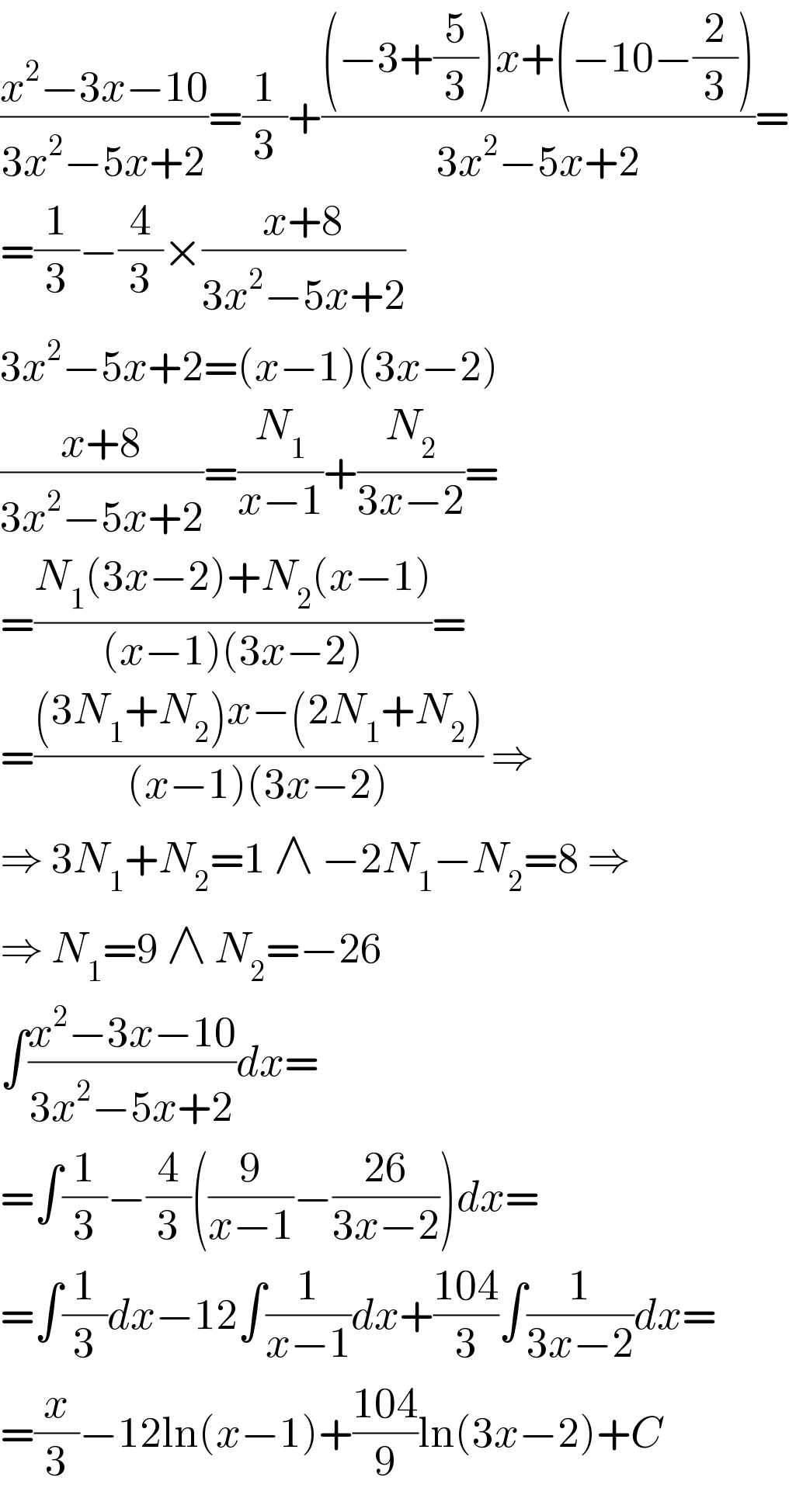
((x^2 −3x−10)/(3x^2 −5x+2))=(1/3)+(((−3+(5/3))x+(−10−(2/3)))/(3x^2 −5x+2))= =(1/3)−(4/3)×((x+8)/(3x^2 −5x+2)) 3x^2 −5x+2=(x−1)(3x−2) ((x+8)/(3x^2 −5x+2))=(N_1 /(x−1))+(N_2 /(3x−2))= =((N_1 (3x−2)+N_2 (x−1))/((x−1)(3x−2)))= =(((3N_1 +N_2 )x−(2N_1 +N_2 ))/((x−1)(3x−2))) ⇒ ⇒ 3N_1 +N_2 =1 ∧ −2N_1 −N_2 =8 ⇒ ⇒ N_1 =9 ∧ N_2 =−26 ∫((x^2 −3x−10)/(3x^2 −5x+2))dx= =∫(1/3)−(4/3)((9/(x−1))−((26)/(3x−2)))dx= =∫(1/3)dx−12∫(1/(x−1))dx+((104)/3)∫(1/(3x−2))dx= =(x/3)−12ln(x−1)+((104)/9)ln(3x−2)+C

$$\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{10}}{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\left(−\mathrm{3}+\frac{\mathrm{5}}{\mathrm{3}}\right){x}+\left(−\mathrm{10}−\frac{\mathrm{2}}{\mathrm{3}}\right)}{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{3}}×\frac{{x}+\mathrm{8}}{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}=\left({x}−\mathrm{1}\right)\left(\mathrm{3}{x}−\mathrm{2}\right) \\ $$$$\frac{{x}+\mathrm{8}}{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}}=\frac{{N}_{\mathrm{1}} }{{x}−\mathrm{1}}+\frac{{N}_{\mathrm{2}} }{\mathrm{3}{x}−\mathrm{2}}= \\ $$$$=\frac{{N}_{\mathrm{1}} \left(\mathrm{3}{x}−\mathrm{2}\right)+{N}_{\mathrm{2}} \left({x}−\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)\left(\mathrm{3}{x}−\mathrm{2}\right)}= \\ $$$$=\frac{\left(\mathrm{3}{N}_{\mathrm{1}} +{N}_{\mathrm{2}} \right){x}−\left(\mathrm{2}{N}_{\mathrm{1}} +{N}_{\mathrm{2}} \right)}{\left({x}−\mathrm{1}\right)\left(\mathrm{3}{x}−\mathrm{2}\right)}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{3}{N}_{\mathrm{1}} +{N}_{\mathrm{2}} =\mathrm{1}\:\wedge\:−\mathrm{2}{N}_{\mathrm{1}} −{N}_{\mathrm{2}} =\mathrm{8}\:\Rightarrow \\ $$$$\Rightarrow\:{N}_{\mathrm{1}} =\mathrm{9}\:\wedge\:{N}_{\mathrm{2}} =−\mathrm{26} \\ $$$$\int\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{10}}{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{2}}{dx}= \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{9}}{{x}−\mathrm{1}}−\frac{\mathrm{26}}{\mathrm{3}{x}−\mathrm{2}}\right){dx}= \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{3}}{dx}−\mathrm{12}\int\frac{\mathrm{1}}{{x}−\mathrm{1}}{dx}+\frac{\mathrm{104}}{\mathrm{3}}\int\frac{\mathrm{1}}{\mathrm{3}{x}−\mathrm{2}}{dx}= \\ $$$$=\frac{{x}}{\mathrm{3}}−\mathrm{12ln}\left({x}−\mathrm{1}\right)+\frac{\mathrm{104}}{\mathrm{9}}\mathrm{ln}\left(\mathrm{3}{x}−\mathrm{2}\right)+{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply