Question Number 32968 by diyatrivedi last updated on 08/Apr/18
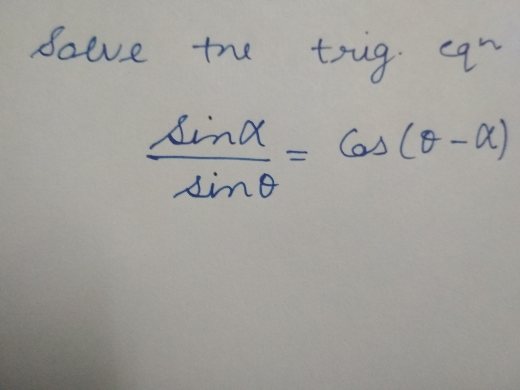
Answered by MJS last updated on 08/Apr/18
![((sin α)/(sin θ))=cos α×cos θ+sin α×sin θ sin α =cos α×cos θ×sin θ+sinα×sin^2 θ sin α=cos α×((sin 2θ)/2)+sin α×(((1−cos 2θ)/2)) ((sin α)/2)=cos α×((sin 2θ)/2)−sin α×((cos 2θ)/2) sin α=((sin (2θ+α)+sin (2θ−α))/2)−((sin (α+2θ)+sin (α−2θ))/2) sin α=sin (2θ−α) α=θ+nπ [θ∈R; n∈Z] or θ=(π/2)+nπ [α∈R; n∈Z]](https://www.tinkutara.com/question/Q32974.png)
$$\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\theta}=\mathrm{cos}\:\alpha×\mathrm{cos}\:\theta+\mathrm{sin}\:\alpha×\mathrm{sin}\:\theta \\ $$$$\mathrm{sin}\:\alpha\:=\mathrm{cos}\:\alpha×\mathrm{cos}\:\theta×\mathrm{sin}\:\theta+\mathrm{sin}\alpha×\mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$\mathrm{sin}\:\alpha=\mathrm{cos}\:\alpha×\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}+\mathrm{sin}\:\alpha×\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{2}}=\mathrm{cos}\:\alpha×\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}−\mathrm{sin}\:\alpha×\frac{\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{sin}\:\left(\mathrm{2}\theta+\alpha\right)+\mathrm{sin}\:\left(\mathrm{2}\theta−\alpha\right)}{\mathrm{2}}−\frac{\mathrm{sin}\:\left(\alpha+\mathrm{2}\theta\right)+\mathrm{sin}\:\left(\alpha−\mathrm{2}\theta\right)}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\alpha=\mathrm{sin}\:\left(\mathrm{2}\theta−\alpha\right) \\ $$$$\alpha=\theta+{n}\pi\:\left[\theta\in\mathbb{R};\:{n}\in\mathbb{Z}\right] \\ $$$$\mathrm{or} \\ $$$$\theta=\frac{\pi}{\mathrm{2}}+{n}\pi\:\left[\alpha\in\mathbb{R};\:{n}\in\mathbb{Z}\right] \\ $$
