Question Number 32985 by soufiane zarik last updated on 08/Apr/18
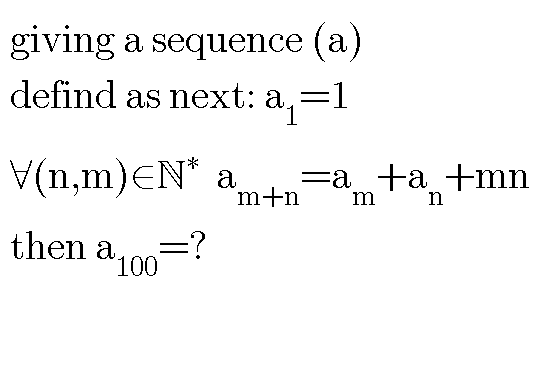
Answered by MJS last updated on 08/Apr/18
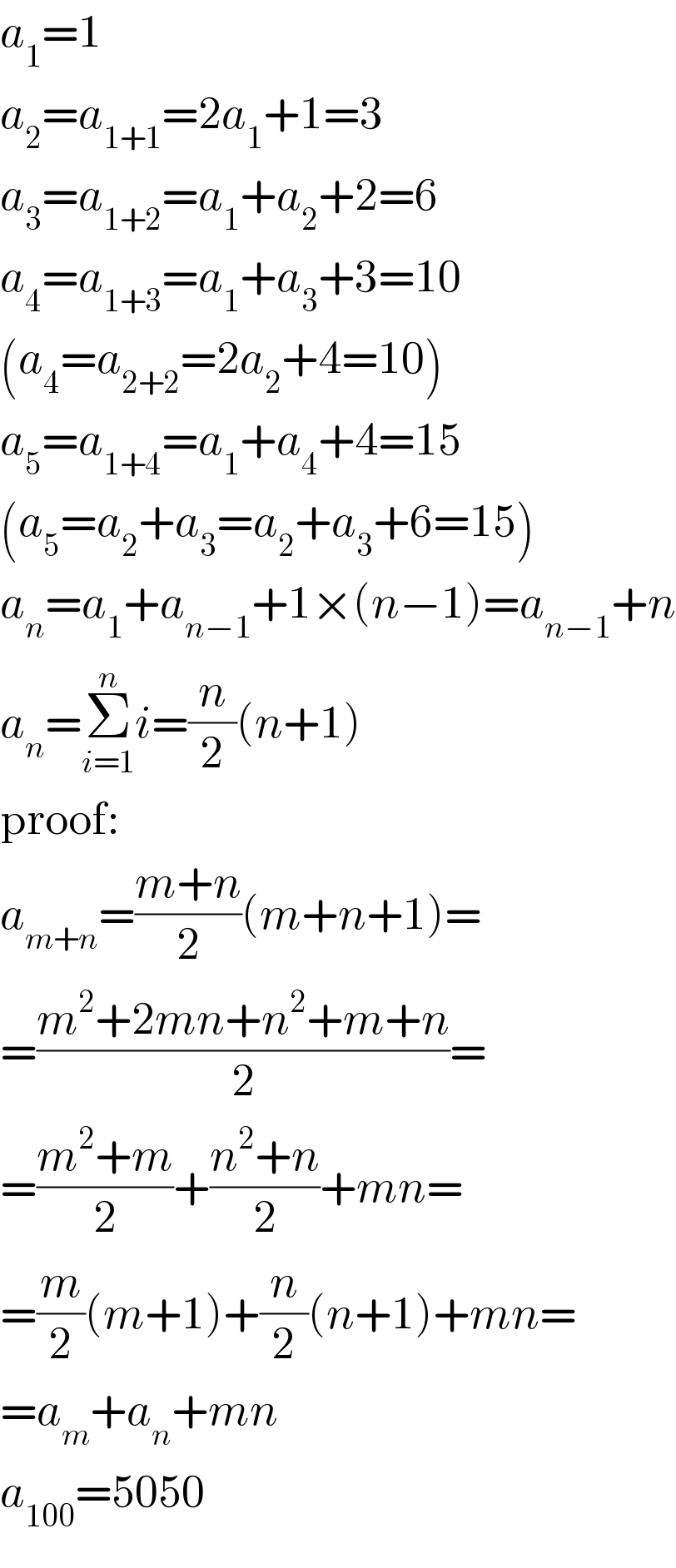
$${a}_{\mathrm{1}} =\mathrm{1} \\ $$$${a}_{\mathrm{2}} ={a}_{\mathrm{1}+\mathrm{1}} =\mathrm{2}{a}_{\mathrm{1}} +\mathrm{1}=\mathrm{3} \\ $$$${a}_{\mathrm{3}} ={a}_{\mathrm{1}+\mathrm{2}} ={a}_{\mathrm{1}} +{a}_{\mathrm{2}} +\mathrm{2}=\mathrm{6} \\ $$$${a}_{\mathrm{4}} ={a}_{\mathrm{1}+\mathrm{3}} ={a}_{\mathrm{1}} +{a}_{\mathrm{3}} +\mathrm{3}=\mathrm{10} \\ $$$$\left({a}_{\mathrm{4}} ={a}_{\mathrm{2}+\mathrm{2}} =\mathrm{2}{a}_{\mathrm{2}} +\mathrm{4}=\mathrm{10}\right) \\ $$$${a}_{\mathrm{5}} ={a}_{\mathrm{1}+\mathrm{4}} ={a}_{\mathrm{1}} +{a}_{\mathrm{4}} +\mathrm{4}=\mathrm{15} \\ $$$$\left({a}_{\mathrm{5}} ={a}_{\mathrm{2}} +{a}_{\mathrm{3}} ={a}_{\mathrm{2}} +{a}_{\mathrm{3}} +\mathrm{6}=\mathrm{15}\right) \\ $$$${a}_{{n}} ={a}_{\mathrm{1}} +{a}_{{n}−\mathrm{1}} +\mathrm{1}×\left({n}−\mathrm{1}\right)={a}_{{n}−\mathrm{1}} +{n} \\ $$$${a}_{{n}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}=\frac{{n}}{\mathrm{2}}\left({n}+\mathrm{1}\right) \\ $$$$\mathrm{proof}: \\ $$$${a}_{{m}+{n}} =\frac{{m}+{n}}{\mathrm{2}}\left({m}+{n}+\mathrm{1}\right)= \\ $$$$=\frac{{m}^{\mathrm{2}} +\mathrm{2}{mn}+{n}^{\mathrm{2}} +{m}+{n}}{\mathrm{2}}= \\ $$$$=\frac{{m}^{\mathrm{2}} +{m}}{\mathrm{2}}+\frac{{n}^{\mathrm{2}} +{n}}{\mathrm{2}}+{mn}= \\ $$$$=\frac{{m}}{\mathrm{2}}\left({m}+\mathrm{1}\right)+\frac{{n}}{\mathrm{2}}\left({n}+\mathrm{1}\right)+{mn}= \\ $$$$={a}_{{m}} +{a}_{{n}} +{mn} \\ $$$${a}_{\mathrm{100}} =\mathrm{5050} \\ $$
Commented by soufiane zarik last updated on 08/Apr/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}\:! \\ $$
