Question Number 32999 by artibunja last updated on 09/Apr/18
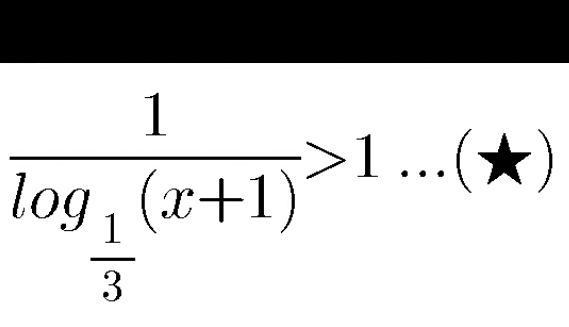
Commented by prof Abdo imad last updated on 09/Apr/18
![⇔ ( ((ln(x+1))/(ln((1/3)))))^(−1) >1 ⇔ ( ((ln(x+1))/(−ln(3))))^(−1) >1 with x>−1 ⇔ − ((ln3)/(ln(x+1))) > 1 ⇔ ((ln3)/(ln(x+1))) <−1 ⇔ ((ln3)/(ln(x+1))) +1 <0 ⇔ ((ln(x+1) +ln(3))/(ln(x+1))) <0 case1 x>0 ⇒x+1>1⇒ln(x+1) >0 (e) ⇔ ln(3x+3) <0 ⇔ 0< 3x+3<1 ⇒−1< x < ((−2)/3) but x>0 so no solution case 2 −1<x<0 (e)⇔ ln(3x+3)>0 ⇔3x+3>1 ⇔ x >−(2/3) ⇒ S_2 =]−(2/3),0[ ⇒ S = S_1 ∪S_2 =]−(2/3),0[ .](https://www.tinkutara.com/question/Q33001.png)
$$\Leftrightarrow\:\:\:\left(\:\:\frac{{ln}\left({x}+\mathrm{1}\right)}{{ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}\right)^{−\mathrm{1}} \:>\mathrm{1}\:\Leftrightarrow\:\left(\:\frac{{ln}\left({x}+\mathrm{1}\right)}{−{ln}\left(\mathrm{3}\right)}\right)^{−\mathrm{1}} \:>\mathrm{1}\:\:{with}\:{x}>−\mathrm{1} \\ $$$$\Leftrightarrow\:−\:\frac{{ln}\mathrm{3}}{{ln}\left({x}+\mathrm{1}\right)}\:>\:\mathrm{1}\:\Leftrightarrow\:\:\frac{{ln}\mathrm{3}}{{ln}\left({x}+\mathrm{1}\right)}\:<−\mathrm{1} \\ $$$$\Leftrightarrow\:\:\frac{{ln}\mathrm{3}}{{ln}\left({x}+\mathrm{1}\right)}\:+\mathrm{1}\:<\mathrm{0}\:\Leftrightarrow\:\:\frac{{ln}\left({x}+\mathrm{1}\right)\:+{ln}\left(\mathrm{3}\right)}{{ln}\left({x}+\mathrm{1}\right)}\:<\mathrm{0} \\ $$$${case}\mathrm{1}\:\:{x}>\mathrm{0}\:\Rightarrow{x}+\mathrm{1}>\mathrm{1}\Rightarrow{ln}\left({x}+\mathrm{1}\right)\:>\mathrm{0}\:\:\left({e}\right)\:\Leftrightarrow \\ $$$$\:{ln}\left(\mathrm{3}{x}+\mathrm{3}\right)\:<\mathrm{0}\:\:\:\Leftrightarrow\:\:\:\mathrm{0}<\:\mathrm{3}{x}+\mathrm{3}<\mathrm{1}\:\Rightarrow−\mathrm{1}<\:{x}\:<\:\frac{−\mathrm{2}}{\mathrm{3}} \\ $$$${but}\:\:{x}>\mathrm{0}\:{so}\:\:{no}\:{solution} \\ $$$${case}\:\mathrm{2}\:−\mathrm{1}<{x}<\mathrm{0}\:\:\left({e}\right)\Leftrightarrow\:{ln}\left(\mathrm{3}{x}+\mathrm{3}\right)>\mathrm{0}\:\:\Leftrightarrow\mathrm{3}{x}+\mathrm{3}>\mathrm{1} \\ $$$$\left.\Leftrightarrow\:{x}\:>−\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\:\:{S}_{\mathrm{2}} \:=\right]−\frac{\mathrm{2}}{\mathrm{3}},\mathrm{0}\left[\:\Rightarrow\:{S}\:=\:{S}_{\mathrm{1}} \cup{S}_{\mathrm{2}} \right. \\ $$$$\left.=\right]−\frac{\mathrm{2}}{\mathrm{3}},\mathrm{0}\left[\:.\right. \\ $$$$ \\ $$
Answered by artibunja last updated on 09/Apr/18

