Question Number 33051 by Tinkutara last updated on 09/Apr/18

Commented by MJS last updated on 09/Apr/18

$$\mathrm{what}'\mathrm{s}\:\mathrm{the}\:\mathrm{eccentric}\:\mathrm{angle}? \\ $$$$\mathrm{is}\:\mathrm{it}\:\angle{F}_{\mathrm{1}} {AF}_{\mathrm{2}} ? \\ $$
Commented by Tinkutara last updated on 10/Apr/18
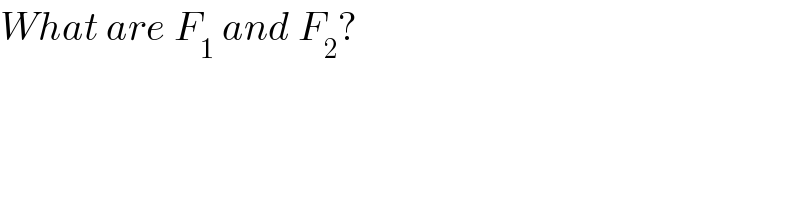
$${What}\:{are}\:{F}_{\mathrm{1}} \:{and}\:{F}_{\mathrm{2}} ? \\ $$
Commented by MJS last updated on 10/Apr/18
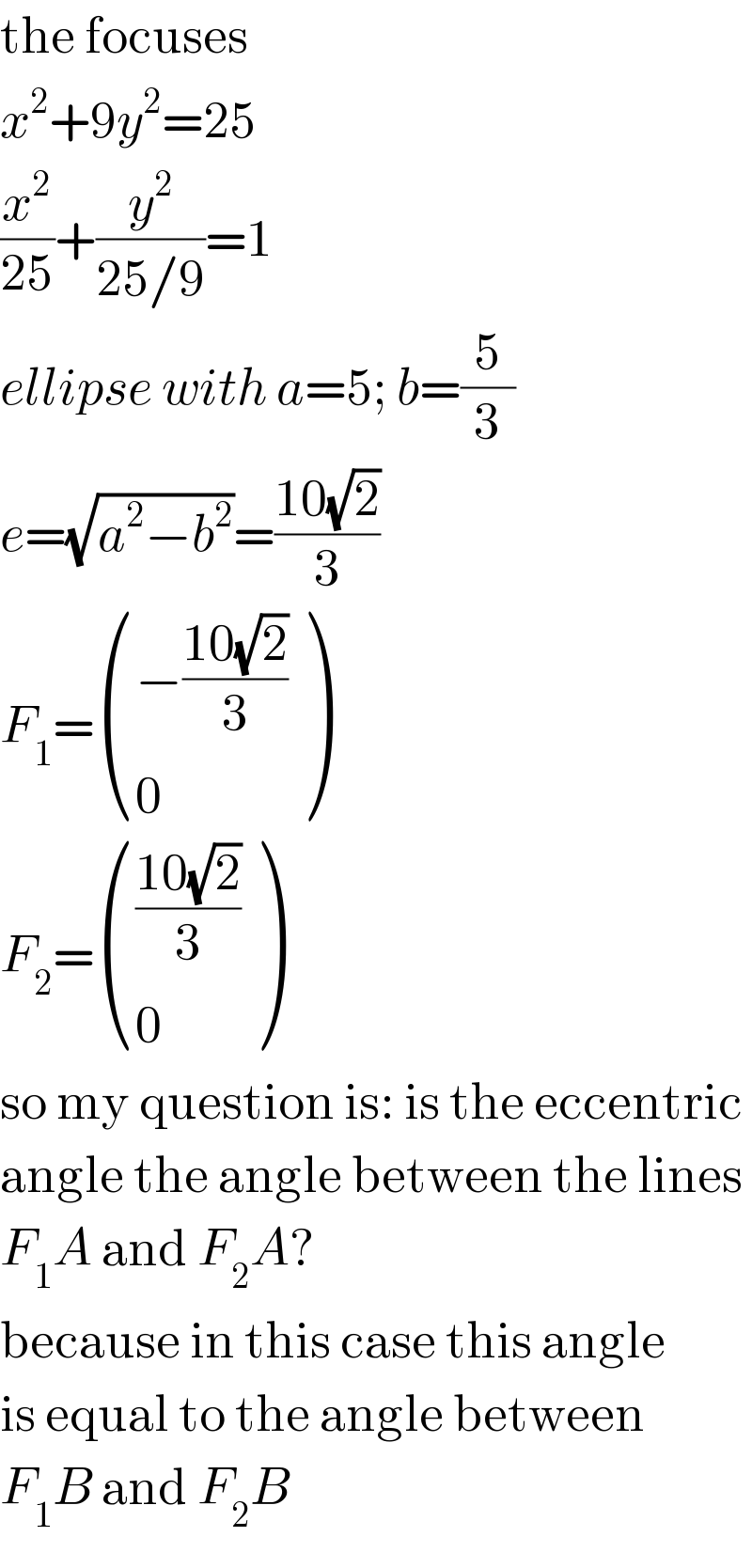
$$\mathrm{the}\:\mathrm{focuses} \\ $$$${x}^{\mathrm{2}} +\mathrm{9}{y}^{\mathrm{2}} =\mathrm{25} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{25}}+\frac{{y}^{\mathrm{2}} }{\mathrm{25}/\mathrm{9}}=\mathrm{1} \\ $$$${ellipse}\:{with}\:{a}=\mathrm{5};\:{b}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${e}=\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }=\frac{\mathrm{10}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$${F}_{\mathrm{1}} =\begin{pmatrix}{−\frac{\mathrm{10}\sqrt{\mathrm{2}}}{\mathrm{3}}}\\{\mathrm{0}}\end{pmatrix} \\ $$$${F}_{\mathrm{2}} =\begin{pmatrix}{\frac{\mathrm{10}\sqrt{\mathrm{2}}}{\mathrm{3}}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{so}\:\mathrm{my}\:\mathrm{question}\:\mathrm{is}:\:\mathrm{is}\:\mathrm{the}\:\mathrm{eccentric} \\ $$$$\mathrm{angle}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{between}\:\mathrm{the}\:\mathrm{lines} \\ $$$${F}_{\mathrm{1}} {A}\:\mathrm{and}\:{F}_{\mathrm{2}} {A}? \\ $$$$\mathrm{because}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{this}\:\mathrm{angle} \\ $$$$\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{between} \\ $$$${F}_{\mathrm{1}} {B}\:\mathrm{and}\:{F}_{\mathrm{2}} {B} \\ $$
