Question Number 33064 by artibunja last updated on 09/Apr/18
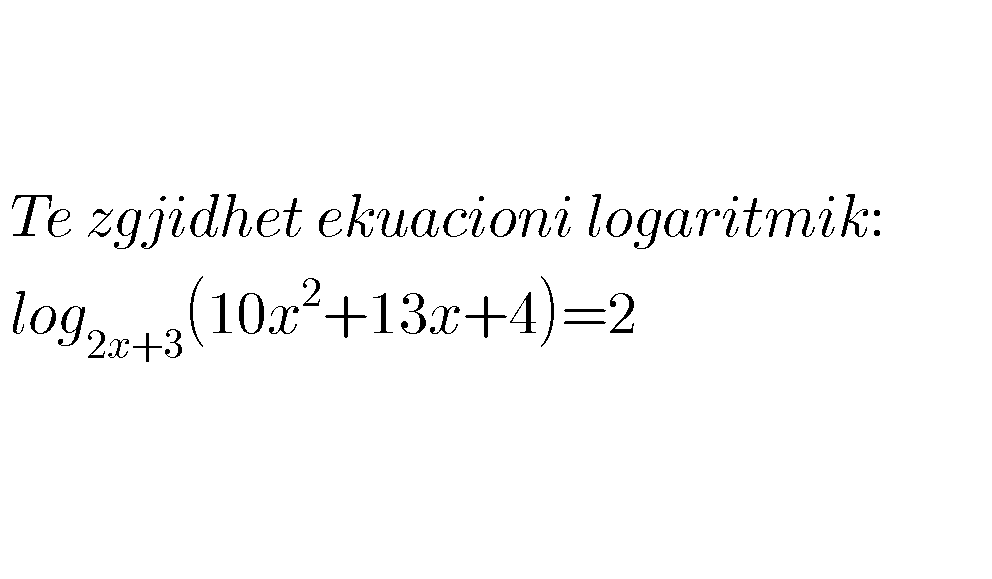
Commented by abdo imad last updated on 09/Apr/18
![we must have 2x+3>0 and 10x^2 +13x +4>0 Δ =13^2 −4 ×10 ×4 =169 −160 =9 >0 x_1 =((−13 +3)/(20))=−(1/2) , x_2 = ((−13 −3)/(20)) =((−16)/(20)) =−(4/5) we must have x∈(]−∞,−(4/5)[∪]−(1/2),+∞[)∩]−(3/2),+∞[ ⇒ x∈]−(3/2),−(4/5)[∪]−(1/2),+∞[ (e)⇔ ((ln(10x^2 +13x +4))/(ln(2x+3))) =2 ⇔ ln(10x^2 +13x +4)=ln((2x+3)^2 )⇔ 10x^2 +13x +4 =4x^2 +12x +9 ⇔ 6x^2 +x −5 =0 Δ =1 −4.6.(−5) =121 ⇒ x_(1 ) =((−1 +11)/(12)) =((10)/(12)) =(5/6) x_2 =((−1−11)/(12)) =−1 but −1 ∈ D_((e)) , (5/6) ∈ D_((e)) ⇒ −1 and (5/6) are the solutions of this equation.](https://www.tinkutara.com/question/Q33070.png)
$${we}\:{must}\:{have}\:\mathrm{2}{x}+\mathrm{3}>\mathrm{0}\:{and}\:\mathrm{10}{x}^{\mathrm{2}} \:+\mathrm{13}{x}\:+\mathrm{4}>\mathrm{0} \\ $$$$\Delta\:=\mathrm{13}^{\mathrm{2}} \:−\mathrm{4}\:×\mathrm{10}\:×\mathrm{4}\:=\mathrm{169}\:−\mathrm{160}\:=\mathrm{9}\:>\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\frac{−\mathrm{13}\:+\mathrm{3}}{\mathrm{20}}=−\frac{\mathrm{1}}{\mathrm{2}}\:,\:{x}_{\mathrm{2}} =\:\frac{−\mathrm{13}\:−\mathrm{3}}{\mathrm{20}}\:=\frac{−\mathrm{16}}{\mathrm{20}}\:=−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\left.{we}\:{must}\:{have}\:{x}\in\left(\right]−\infty,−\frac{\mathrm{4}}{\mathrm{5}}\left[\cup\right]−\frac{\mathrm{1}}{\mathrm{2}},+\infty\left[\right)\cap\right]−\frac{\mathrm{3}}{\mathrm{2}},+\infty\left[\right. \\ $$$$\left.\Rightarrow\:{x}\in\right]−\frac{\mathrm{3}}{\mathrm{2}},−\frac{\mathrm{4}}{\mathrm{5}}\left[\cup\right]−\frac{\mathrm{1}}{\mathrm{2}},+\infty\left[\right. \\ $$$$\left({e}\right)\Leftrightarrow\:\frac{{ln}\left(\mathrm{10}{x}^{\mathrm{2}} \:+\mathrm{13}{x}\:+\mathrm{4}\right)}{{ln}\left(\mathrm{2}{x}+\mathrm{3}\right)}\:=\mathrm{2}\:\Leftrightarrow \\ $$$${ln}\left(\mathrm{10}{x}^{\mathrm{2}} \:+\mathrm{13}{x}\:+\mathrm{4}\right)={ln}\left(\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} \right)\Leftrightarrow \\ $$$$\mathrm{10}{x}^{\mathrm{2}} \:+\mathrm{13}{x}\:+\mathrm{4}\:=\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{12}{x}\:+\mathrm{9}\:\Leftrightarrow \\ $$$$\mathrm{6}{x}^{\mathrm{2}} \:+{x}\:−\mathrm{5}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{1}\:−\mathrm{4}.\mathrm{6}.\left(−\mathrm{5}\right)\:=\mathrm{121}\:\Rightarrow\:{x}_{\mathrm{1}\:} =\frac{−\mathrm{1}\:+\mathrm{11}}{\mathrm{12}}\:=\frac{\mathrm{10}}{\mathrm{12}}\:=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$${x}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{11}}{\mathrm{12}}\:=−\mathrm{1}\:\:\:{but}\:\:−\mathrm{1}\:\in\:{D}_{\left({e}\right)} \:,\:\frac{\mathrm{5}}{\mathrm{6}}\:\in\:{D}_{\left({e}\right)} \:\Rightarrow \\ $$$$−\mathrm{1}\:{and}\:\frac{\mathrm{5}}{\mathrm{6}}\:{are}\:{the}\:{solutions}\:{of}\:{this}\:{equation}. \\ $$
Commented by abdo imad last updated on 09/Apr/18
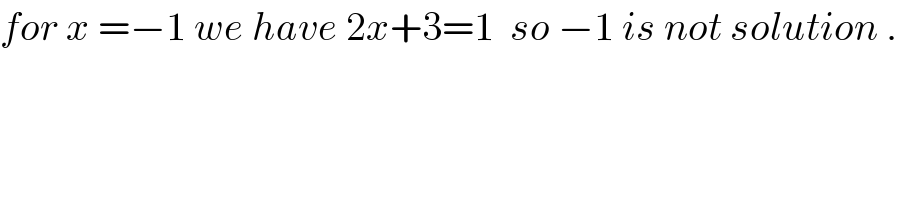
$${for}\:{x}\:=−\mathrm{1}\:{we}\:{have}\:\mathrm{2}{x}+\mathrm{3}=\mathrm{1}\:\:{so}\:−\mathrm{1}\:{is}\:{not}\:{solution}\:. \\ $$
Answered by Rasheed.Sindhi last updated on 10/Apr/18
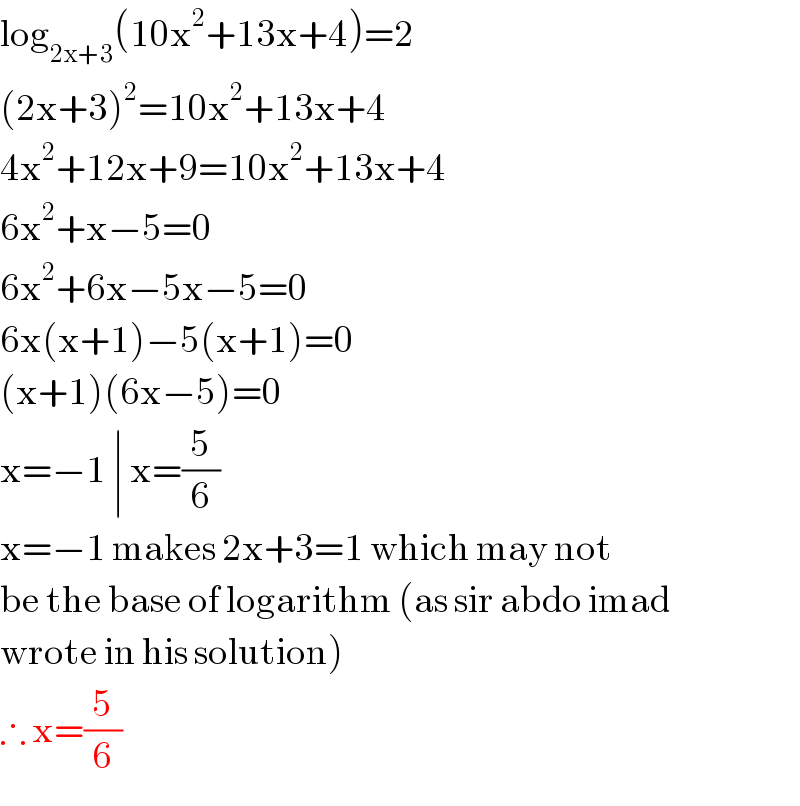
$$\mathrm{log}_{\mathrm{2x}+\mathrm{3}} \left(\mathrm{10x}^{\mathrm{2}} +\mathrm{13x}+\mathrm{4}\right)=\mathrm{2} \\ $$$$\left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{2}} =\mathrm{10x}^{\mathrm{2}} +\mathrm{13x}+\mathrm{4} \\ $$$$\mathrm{4x}^{\mathrm{2}} +\mathrm{12x}+\mathrm{9}=\mathrm{10x}^{\mathrm{2}} +\mathrm{13x}+\mathrm{4} \\ $$$$\mathrm{6x}^{\mathrm{2}} +\mathrm{x}−\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{6x}^{\mathrm{2}} +\mathrm{6x}−\mathrm{5x}−\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{6x}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{5}\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{6x}−\mathrm{5}\right)=\mathrm{0} \\ $$$$\mathrm{x}=−\mathrm{1}\:\mid\:\mathrm{x}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\mathrm{x}=−\mathrm{1}\:\mathrm{makes}\:\mathrm{2x}+\mathrm{3}=\mathrm{1}\:\mathrm{which}\:\mathrm{may}\:\mathrm{not} \\ $$$$\mathrm{be}\:\mathrm{the}\:\mathrm{base}\:\mathrm{of}\:\mathrm{logarithm}\:\left(\mathrm{as}\:\mathrm{sir}\:\mathrm{abdo}\:\mathrm{imad}\right. \\ $$$$\left.\mathrm{wrote}\:\mathrm{in}\:\mathrm{his}\:\mathrm{solution}\right) \\ $$$$\therefore\:\mathrm{x}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$
