Question Number 33100 by artibunja last updated on 10/Apr/18
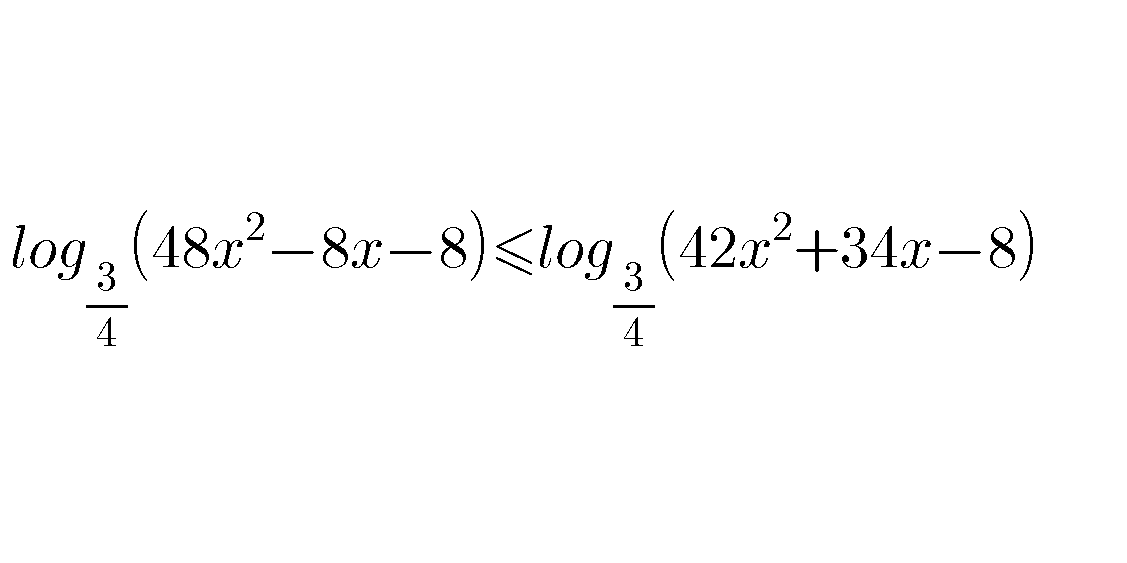
Answered by MJS last updated on 10/Apr/18

$$\mathrm{48}{x}^{\mathrm{2}} −\mathrm{8}{x}−\mathrm{8}>\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{x}<−\frac{\mathrm{1}}{\mathrm{3}}\vee{x}>\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{42}{x}^{\mathrm{2}} +\mathrm{34}{x}−\mathrm{8}>\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{x}<−\mathrm{1}\vee{x}>\frac{\mathrm{4}}{\mathrm{21}} \\ $$$$ \\ $$$$\Rightarrow{x}<−\mathrm{1}\vee{x}>\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\frac{\mathrm{ln}\left(\mathrm{48}{x}^{\mathrm{2}} −\mathrm{8}{x}−\mathrm{8}\right)}{\mathrm{ln}\:\frac{\mathrm{3}}{\mathrm{4}}}\leqslant\frac{\mathrm{ln}\left(\mathrm{42}{x}^{\mathrm{2}} +\mathrm{34}{x}−\mathrm{8}\right)}{\mathrm{ln}\:\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\mathrm{ln}\left(\mathrm{48}{x}^{\mathrm{2}} −\mathrm{8}{x}−\mathrm{8}\right)\geqslant\mathrm{ln}\left(\mathrm{42}{x}^{\mathrm{2}} +\mathrm{34}{x}−\mathrm{8}\right) \\ $$$$\mathrm{48}{x}^{\mathrm{2}} −\mathrm{8}{x}−\mathrm{8}\geqslant\mathrm{42}{x}^{\mathrm{2}} +\mathrm{34}{x}−\mathrm{8} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} −\mathrm{42}{x}\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{7}\right){x}\geqslant\mathrm{0} \\ $$$${x}\geqslant\mathrm{0}\wedge\left({x}−\mathrm{7}\right)\geqslant\mathrm{0}\:\Rightarrow\:{x}\geqslant\mathrm{7} \\ $$$${x}\leqslant\mathrm{0}\wedge\left({x}−\mathrm{7}\right)\leqslant\mathrm{0}\:\Rightarrow\:{x}\leqslant\mathrm{0} \\ $$$$ \\ $$$$\mathrm{answer}\:\mathrm{is} \\ $$$${x}<−\mathrm{1}\vee{x}\geqslant\mathrm{7} \\ $$
