Question-33103

Question Number 33103 by mondodotto@gmail.com last updated on 10/Apr/18

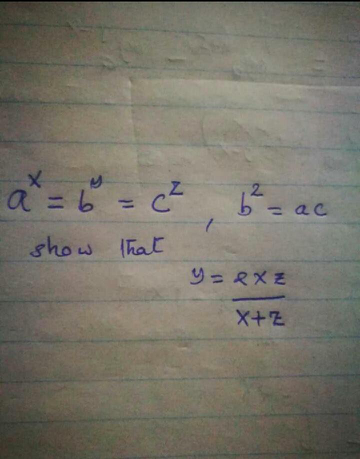
Commented by Rasheed.Sindhi last updated on 10/Apr/18

$$\mathrm{x}=\mathrm{y}=\mathrm{z}=\mathrm{0} \\ $$$$\mathrm{In}\:\mathrm{this}\:\mathrm{case}\:\mathrm{y}\neq\frac{\mathrm{2xz}}{\mathrm{x}+\mathrm{z}} \\ $$

Answered by MJS last updated on 10/Apr/18

1.: b^2 =ac ⇒ a=(b^2 /c) 2.: b^y =c^z ⇒ c=b^(y/z) 3. (2. in 1.): a=(b^2 /b^(y/z) )=b^(2−(y/z)) =b^((2z−y)/z) 4.: a^x =b^y ⇒ y=x((ln a)/(ln b)) 3. in 4.: y=x((ln b^((2z−y)/z) )/(ln b)) y=x(((((2z−y)/z))ln b)/(ln b)) y=((2xz−xy)/z) y=((2xz)/(x+z))

$$\mathrm{1}.:\:{b}^{\mathrm{2}} ={ac}\:\Rightarrow\:{a}=\frac{{b}^{\mathrm{2}} }{{c}} \\ $$$$\mathrm{2}.:\:{b}^{{y}} ={c}^{{z}} \:\Rightarrow\:{c}={b}^{\frac{{y}}{{z}}} \\ $$$$\mathrm{3}.\:\left(\mathrm{2}.\:\mathrm{in}\:\mathrm{1}.\right):\:{a}=\frac{{b}^{\mathrm{2}} }{{b}^{\frac{{y}}{{z}}} }={b}^{\mathrm{2}−\frac{{y}}{{z}}} ={b}^{\frac{\mathrm{2}{z}−{y}}{{z}}} \\ $$$$\mathrm{4}.:\:{a}^{{x}} ={b}^{{y}} \:\Rightarrow\:{y}={x}\frac{\mathrm{ln}\:{a}}{\mathrm{ln}\:{b}} \\ $$$$\mathrm{3}.\:\mathrm{in}\:\mathrm{4}.:\:{y}={x}\frac{\mathrm{ln}\:{b}^{\frac{\mathrm{2}{z}−{y}}{{z}}} }{\mathrm{ln}\:{b}} \\ $$$${y}={x}\frac{\left(\frac{\mathrm{2}{z}−{y}}{{z}}\right)\mathrm{ln}\:{b}}{\mathrm{ln}\:{b}} \\ $$$${y}=\frac{\mathrm{2}{xz}−{xy}}{{z}} \\ $$$${y}=\frac{\mathrm{2}{xz}}{{x}+{z}} \\ $$

Facebook Tweet Pin

Question-33103

Leave a Reply Cancel reply