Question Number 33214 by Tinkutara last updated on 13/Apr/18

Commented by Tinkutara last updated on 13/Apr/18

Commented by Tinkutara last updated on 15/Apr/18
But if we consider the torque of mg instead of ma it still gives approximately the same answer. Which one is conceptually correct?
Commented by ajfour last updated on 14/Apr/18
Commented by ajfour last updated on 14/Apr/18
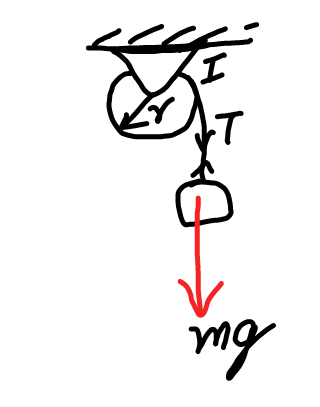
![mg−T=ma TR=I((a/R)) ⇒ mg=a[m+(I/R^2 )] ...(1) s=(1/2)at^2 ⇒ a=((2s)/t^2 ) using in (1) mg=((2s)/t^2 )(m+(I/R^2 )) or I = (((mgt^2 )/(2s))−m)R^2 =(((0.5×10×16)/(2×1.5))−0.5)(0.15)^2 =(((80)/3)−0.5)(0.0225)kg.m^2 =(((80)/3)−(1/2))((9/(400))) kg.m^2 =((157)/6)×(9/(400)) =((157×3)/(800)) = ((4.71)/8) = 0.59 kg.m^2 .](https://www.tinkutara.com/question/Q33326.png)
$${mg}−{T}={ma} \\ $$$${TR}={I}\left(\frac{{a}}{{R}}\right) \\ $$$$\Rightarrow\:\:\:{mg}={a}\left[{m}+\frac{{I}}{{R}^{\mathrm{2}} }\right]\:\:\:\:…\left(\mathrm{1}\right) \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{2}}{at}^{\mathrm{2}} \:\:\:\Rightarrow\:\:\:{a}=\frac{\mathrm{2}{s}}{{t}^{\mathrm{2}} } \\ $$$${using}\:{in}\:\left(\mathrm{1}\right) \\ $$$${mg}=\frac{\mathrm{2}{s}}{{t}^{\mathrm{2}} }\left({m}+\frac{{I}}{{R}^{\mathrm{2}} }\right) \\ $$$${or}\:\:\:\:{I}\:=\:\left(\frac{{mgt}^{\mathrm{2}} }{\mathrm{2}{s}}−{m}\right){R}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left(\frac{\mathrm{0}.\mathrm{5}×\mathrm{10}×\mathrm{16}}{\mathrm{2}×\mathrm{1}.\mathrm{5}}−\mathrm{0}.\mathrm{5}\right)\left(\mathrm{0}.\mathrm{15}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\left(\frac{\mathrm{80}}{\mathrm{3}}−\mathrm{0}.\mathrm{5}\right)\left(\mathrm{0}.\mathrm{0225}\right){kg}.{m}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\left(\frac{\mathrm{80}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{9}}{\mathrm{400}}\right)\:{kg}.{m}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{157}}{\mathrm{6}}×\frac{\mathrm{9}}{\mathrm{400}}\:=\frac{\mathrm{157}×\mathrm{3}}{\mathrm{800}}\:=\:\frac{\mathrm{4}.\mathrm{71}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:=\:\mathrm{0}.\mathrm{59}\:{kg}.{m}^{\mathrm{2}} \:\:. \\ $$
Commented by ajfour last updated on 15/Apr/18

$${if}\:{torque}\:{of}\:{mg}\:{is}\:{taken}\:\:{net} \\ $$$${moment}\:{of}\:{inertia}\:{of}\:{system} \\ $$$${about}\:{fixed}\:{axis}\:{of}\:{pulley}\:{is} \\ $$$${I}_{{system}} ={I}+{mR}^{\mathrm{2}} \\ $$$${mgR}=\left({I}+{mR}^{\mathrm{2}} \right)\left(\frac{{a}}{{R}}\right)\:\:. \\ $$
Commented by Tinkutara last updated on 15/Apr/18
Both are same in value approximately. Which is correct then?
Commented by ajfour last updated on 15/Apr/18
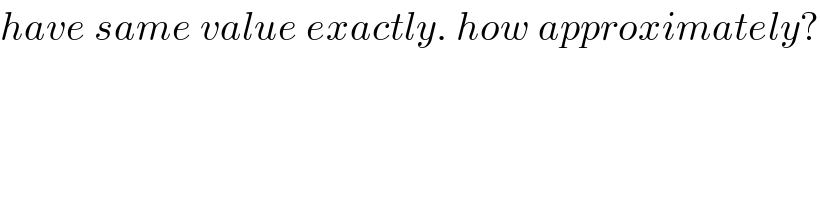
$${have}\:{same}\:{value}\:{exactly}.\:{how}\:{approximately}? \\ $$
Commented by Tinkutara last updated on 15/Apr/18
Thank you very much Sir! I got the answer. ��������
