Question Number 33330 by artibunja last updated on 14/Apr/18
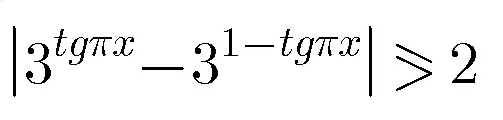
Answered by MJS last updated on 15/Apr/18
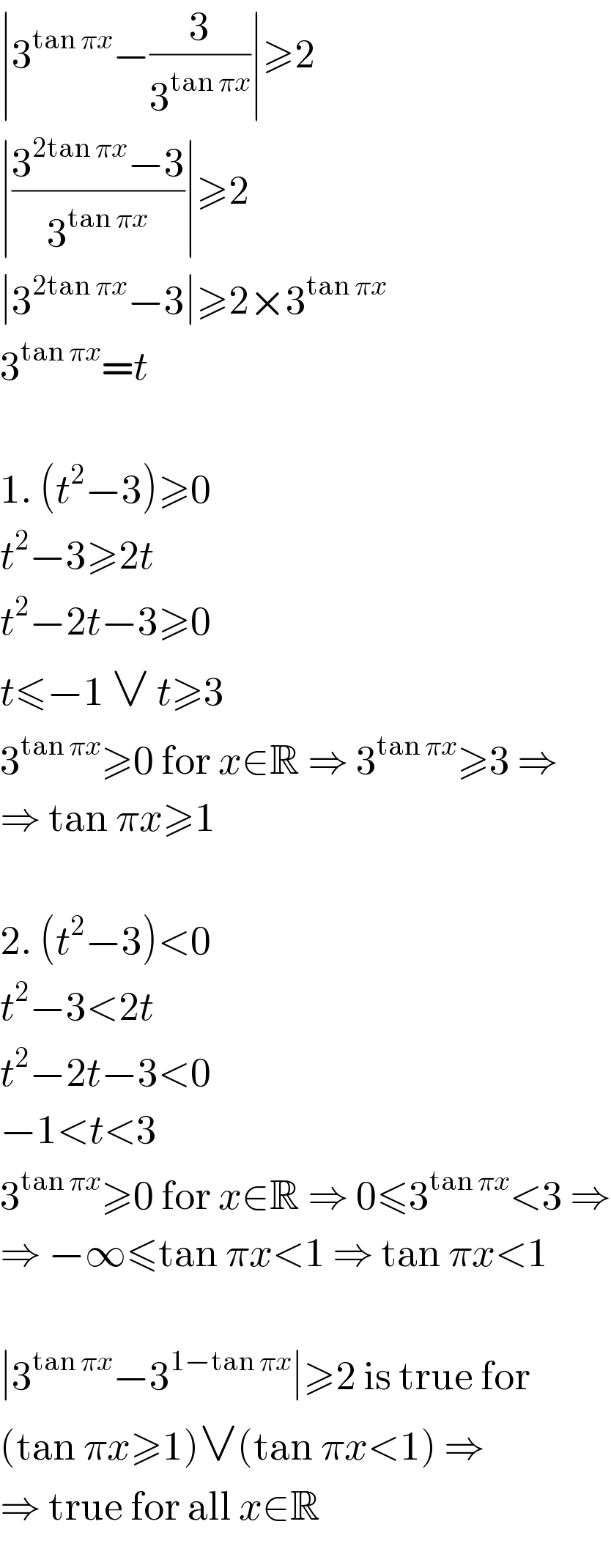
$$\mid\mathrm{3}^{\mathrm{tan}\:\pi{x}} −\frac{\mathrm{3}}{\mathrm{3}^{\mathrm{tan}\:\pi{x}} }\mid\geqslant\mathrm{2} \\ $$$$\mid\frac{\mathrm{3}^{\mathrm{2tan}\:\pi{x}} −\mathrm{3}}{\mathrm{3}^{\mathrm{tan}\:\pi{x}} }\mid\geqslant\mathrm{2} \\ $$$$\mid\mathrm{3}^{\mathrm{2tan}\:\pi{x}} −\mathrm{3}\mid\geqslant\mathrm{2}×\mathrm{3}^{\mathrm{tan}\:\pi{x}} \\ $$$$\mathrm{3}^{\mathrm{tan}\:\pi{x}} ={t} \\ $$$$ \\ $$$$\mathrm{1}.\:\left({t}^{\mathrm{2}} −\mathrm{3}\right)\geqslant\mathrm{0} \\ $$$${t}^{\mathrm{2}} −\mathrm{3}\geqslant\mathrm{2}{t} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{3}\geqslant\mathrm{0} \\ $$$${t}\leqslant−\mathrm{1}\:\vee\:{t}\geqslant\mathrm{3} \\ $$$$\mathrm{3}^{\mathrm{tan}\:\pi{x}} \geqslant\mathrm{0}\:\mathrm{for}\:{x}\in\mathbb{R}\:\Rightarrow\:\mathrm{3}^{\mathrm{tan}\:\pi{x}} \geqslant\mathrm{3}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{tan}\:\pi{x}\geqslant\mathrm{1} \\ $$$$ \\ $$$$\mathrm{2}.\:\left({t}^{\mathrm{2}} −\mathrm{3}\right)<\mathrm{0} \\ $$$${t}^{\mathrm{2}} −\mathrm{3}<\mathrm{2}{t} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{3}<\mathrm{0} \\ $$$$−\mathrm{1}<{t}<\mathrm{3} \\ $$$$\mathrm{3}^{\mathrm{tan}\:\pi{x}} \geqslant\mathrm{0}\:\mathrm{for}\:{x}\in\mathbb{R}\:\Rightarrow\:\mathrm{0}\leqslant\mathrm{3}^{\mathrm{tan}\:\pi{x}} <\mathrm{3}\:\Rightarrow \\ $$$$\Rightarrow\:−\infty\leqslant\mathrm{tan}\:\pi{x}<\mathrm{1}\:\Rightarrow\:\mathrm{tan}\:\pi{x}<\mathrm{1} \\ $$$$ \\ $$$$\mid\mathrm{3}^{\mathrm{tan}\:\pi{x}} −\mathrm{3}^{\mathrm{1}−\mathrm{tan}\:\pi{x}} \mid\geqslant\mathrm{2}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for} \\ $$$$\left(\mathrm{tan}\:\pi{x}\geqslant\mathrm{1}\right)\vee\left(\mathrm{tan}\:\pi{x}<\mathrm{1}\right)\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:{x}\in\mathbb{R} \\ $$
Answered by artibunja last updated on 17/Apr/18

